Galaxy Classification with a Neural Net from Scratch#
Here we implement a neural network from scratch with a single hidden layer, using only NumPy and use it to classify galaxies.
import numpy as np
import matplotlib.pyplot as plt
import h5py
We need the Galaxy class we previously defined
galaxy_types = {0: "disturbed galaxies",
1: "merging galaxies",
2: "round smooth galaxies",
3: "in-between round smooth galaxies",
4: "cigar shaped smooth galaxies",
5: "barred spiral galaxies",
6: "unbarred tight spiral galaxies",
7: "unbarred loose spiral galaxies",
8: "edge-on galaxies without bulge",
9: "edge-on galaxies with bulge"}
class Galaxy:
def __init__(self, data, answer, *, index=-1):
self.data = np.array(data, dtype=np.float32) / 255.0 * 0.99 + 0.01
self.answer = answer
self.out = np.zeros(10, dtype=np.float32) + 0.01
self.out[self.answer] = 0.99
self.index = index
def plot(self, ax=None):
if ax is None:
fig, ax = plt.subplots()
ax.imshow(self.data, interpolation="nearest")
ax.text(0.025, 0.95, f"answer: {self.answer}",
color="white", transform=ax.transAxes)
def validate(self, prediction):
"""check if a categorical prediction matches the answer"""
return np.argmax(prediction) == self.answer
A manager class#
We’ll create a class to manage access to the data. This will do the following:
open the file and store the handles to access the data
partition the data into test and training sets
provide a means to shuffle the data
provide methods to get the next dataset (either training or test)
allow us to coarsen the images to a reduced resolution to make the training easier.
class DataManager:
def __init__(self, partition=0.8,
datafile="Galaxy10_DECals.h5",
coarsen=1):
"""manage access to the data
partition: fraction that should be training
datafile: name of the hdf5 file with the data
coarsen: reduce the number of pixels by this factor
"""
self.ds = h5py.File(datafile)
self.ans = np.array(self.ds["ans"])
self.images = np.array(self.ds["images"])
self.coarsen = coarsen
N = len(self.ans)
# create a set of indices for the galaxies and randomize
self.indices = np.arange(N, dtype=np.uint32)
self.rng = np.random.default_rng()
self.rng.shuffle(self.indices)
# partition into training and test sets
# these indices will always refer to the index in the original
# unsplit dataset
n_cut = int(partition * N)
self.training_indices = self.indices[0:n_cut]
self.test_indices = self.indices[n_cut:N]
self.n_training = len(self.training_indices)
self.n_test = len(self.test_indices)
# store the current index into the *_indices array we are
# accessing
self.curr_idx_train = -1
self.curr_idx_test = -1
def _get_galaxy(self, index):
"""return a numpy array containing a single galaxy image, coarsened
if necessary by averaging"""
_tmp = self.images[index, :, :, :]
if self.coarsen > 1:
_tmp = np.mean(_tmp.reshape(_tmp.shape[0]//self.coarsen, self.coarsen,
_tmp.shape[1]//self.coarsen, self.coarsen,
_tmp.shape[2]), axis=(1, 3))
return _tmp
def get_next_training_image(self):
self.curr_idx_train += 1
if self.curr_idx_train < len(self.training_indices):
idx = self.training_indices[self.curr_idx_train]
return Galaxy(self._get_galaxy(idx), self.ans[idx], index=idx)
return None
def reset_training(self):
"""prepare for the next epoch: shuffle the training data and
reset the index to point to the start"""
self.curr_idx_train = -1
self.rng.shuffle(self.training_indices)
def reset_testing(self):
"""reset the pointer for the test data"""
self.curr_idx_test = -1
def get_next_test_image(self):
self.curr_idx_test += 1
if self.curr_idx_test < len(self.test_indices):
idx = self.test_indices[self.curr_idx_test]
return Galaxy(self._get_galaxy(idx), self.ans[idx], index=idx)
return None
Tip
The get_next_training_image() and get_next_test_image() will return None when there are no more galaxies.
This allows us to loop over the data set as:
d = DataManager()
while g := d.get_next_training_image():
# do stuff with g
where we use the python walrus operator, := to assign to g within the
loop conditional.
We can now work with the data as follows. Here we create a DataManager that will coarsen the images by a factor of 4 (so they will be 64x64 pixels with 3 colors).
d = DataManager(coarsen=4)
we can see how many images there are in the training and test sets
d.n_training, d.n_test
(14188, 3548)
We can then get a training galaxy and look at it:
g = d.get_next_test_image()
g.plot()
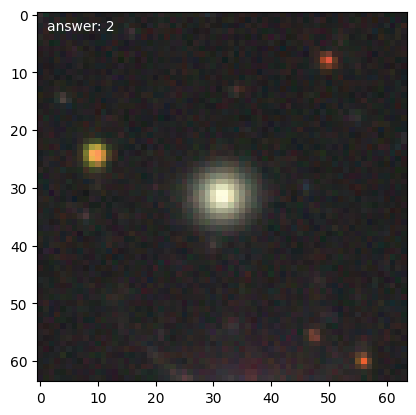
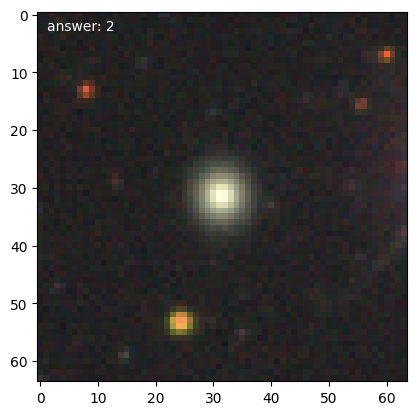
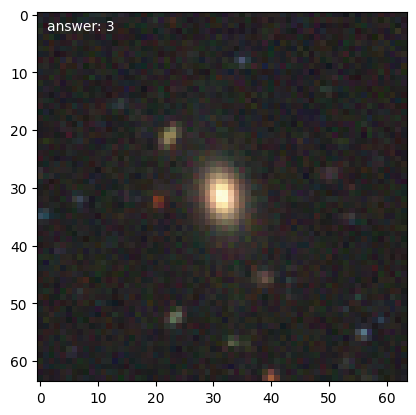
We’ll need a 1-d representation of the data, which we can get using np.ravel()
np.ravel(g.data).shape
(12288,)
Batching#
Training with this data will be very slow. We can speed it up more by using batching and aggregating the linear algebra. Here’s how this works.
Single input recap#
Our basic network does:
where the sizes of the matrices and vectors are:
\({\bf x}^k\) : \(N_\mathrm{in} \times 1\)
\({\bf B}\) : \(N_\mathrm{hidden} \times N_\mathrm{in}\)
\(\tilde{\bf z}^k\) : \(N_\mathrm{hidden}\times 1\)
\({\bf A}\) : \(N_\mathrm{out} \times N_\mathrm{hidden}\)
\({\bf z}^k\) : \(N_\mathrm{out} \times 1\)
we also have the known output, \({\bf y}^k\) corresponding to input \({\bf x}^k\)
\({\bf y}^k\) : \(N_\mathrm{out} \times 1\)
we then compute the errors:
\({\bf e}^k = {\bf z}^k - {\bf y}^k\) (the error on the output layer) : \(N_\mathrm{out} \times 1\)
\(\tilde{\bf e}^k = {\bf A}^\intercal \cdot [{\bf e}^k \circ {\bf z} \circ (1 - {\bf z})]\) (the error backpropagated to the hidden layer) : \(N_\mathrm{hidden} \times 1\)
and finally the corrections due to this single piece of training data, \(({\bf x}^k, {\bf y}^k)\):
\(\Delta {\bf A} = -2\eta \,{\bf e}^k \circ {\bf z}^k \circ (1 - {\bf z}^k) \cdot (\tilde{\bf z}^k)^\intercal\) : \(N_\mathrm{out} \times N_\mathrm{hidden}\)
\(\Delta {\bf B} = -2\eta \,\tilde{\bf e}^k \circ \tilde{\bf z}^k \circ (1 - \tilde{\bf z}^k) \cdot ({\bf x}^k)^\intercal\) : \(N_\mathrm{hidden} \times N_\mathrm{in}\)
A batching approach#
We now want to batch the inputs, by extending \({\bf x}\) to be of size \(N_\mathrm{in} \times S\), where \(S\) is the batch size. This means that each column is a unique input vector \({\bf x}^k\), and \(S\) of them are sandwiched together:
Similarly, we create a batched \({\bf y}_b\) that contains the \({\bf y}^k\) corresponding to the \({\bf x}^k\) in \({\bf x}_b\).
We can propagate this through the network, getting
where \({\bf z}_b\) is now of size \(N_\mathrm{out} \times S\).
Now, we compute the errors from the batched inputs
\({\bf e}_b = {\bf z}_b - {\bf y}_b\) : \(N_\mathrm{out} \times S\)
\(\tilde{\bf e}_b =\underbrace{{\bf A}^\intercal}_{N_\mathrm{hidden} \times N_\mathrm{out}} \cdot \underbrace{[{\bf e}_b \circ {\bf z}_b \circ (1 - {\bf z})]}_{N_\mathrm{out} \times S}\) : \(N_\mathrm{hidden} \times S\)
and the accumulated corrections:
\(\Delta {\bf A} = -\frac{2\eta}{S} \,\underbrace{{\bf e}_b \circ {\bf z}_b \circ (1 - {\bf z}_b)}_{N_\mathrm{out}\times S} \cdot \underbrace{(\tilde{\bf z}_b)^\intercal}_{S\times N_\mathrm{hidden}}\)
\(\Delta {\bf B} = -\frac{2\eta}{S} \,\underbrace{\tilde{\bf e}_b \circ \tilde{\bf z}_b \circ (1 - \tilde{\bf z}_b)}_{N_\mathrm{hidden} \times S} \cdot \underbrace{({\bf x}_b)^\intercal}_{S \times N_\mathrm{in}}\)
In these accumulated corrections, the \(S\) dimensions contract. In essence, this means that each element in \(\Delta {\bf A}\) and \(\Delta {\bf B}\) is the sum of the corrections for each of the \(S\) training data pairs in the batch. For this reason, we normalize by \(S\) to create the average of the gradient.
Tip
Batching also stabilizes the gradient descent, making it easier to find the minimum and allowing us to use a larger learning rate.
Momentum#
The other feature we need for this application is momentum in the gradient descent weight updates.
A popular form of momentum (see, e.g., Momentum: A simple, yet efficient optimizing technique) builds off of the idea of the exponential moving average.
For our gradient descent update, we usually do:
where \(\mathcal{L}\) is our loss function and \(\eta\) is the learning rate.
The basic idea of momentum begins with defining a “velocity”, \({\bf v}^{(0)} = 0\) (no momentum has been built up yet). Then each iteration of training we do the following:
construct the gradient from the current set of training, \(\partial \mathcal{L}/\partial {\bf A}\)
blend this with the previous momentum using an exponential moving average:
\[{\bf v}^{(i)} = \beta {\bf v}^{(i-1)} + (1 - \beta) \frac{\partial \mathcal{L}}{\partial {\bf A}}\]where \(\beta \in [0, 1]\) is the smoothing parameter. It seems like \(\beta = 0.9\) is used often.
Since every gradient is always multiplied by \((1-\beta)\), and each previous gradient picks up a factor of \(\beta\) each iteration, this construction weights the most recent gradients most.
update the weights:
\[{\bf A} = {\bf A} - \eta {\bf v}^{(i)}\]
We would do the same with the other weights, \({\bf B}\).
Tip
Momentum greatly reduces the swings in the “fraction correct” metric from one epoch to the next.
Implementing our neural network#
We’ll write our network to take a DataManager—it can get everything that it needs from there.
Tip
We also have our network do the validation against the test set each epoch so we can see how well we are doing.
import time
class NeuralNetwork:
"""A neural network class with a single hidden layer."""
def __init__(self, data_manager, *, hidden_layer_size=20):
self.data_manager = data_manager
# let's get the first image from the training set and
# use that to set the sizes
g = self.data_manager.get_next_training_image()
# the number of nodes/neurons on the output layer
self.N_out = g.out.size
# the number of nodes/neurons on the input layer
self.N_in = np.ravel(g.data).size
# the number of nodes/neurons on the hidden layer
self.N_hidden = hidden_layer_size
# we will initialize the weights with Gaussian normal random
# numbers centered on 0 with a width of 1/sqrt(n), where n is
# the length of the input state
rng = np.random.default_rng()
# A is the set of weights between the hidden layer and output layer
self.A = np.zeros((self.N_out, self.N_hidden), dtype=np.float32)
self.A[:, :] = rng.normal(0.0, 1.0/np.sqrt(self.N_hidden), self.A.shape)
# B is the set of weights between the input layer and hidden layer
self.B = np.zeros((self.N_hidden, self.N_in), dtype=np.float32)
self.B[:, :] = rng.normal(0.0, 1.0/np.sqrt(self.N_in), self.B.shape)
# reset the training
self.data_manager.reset_training()
self.n_trained = 0
self.training_time = 0
def sigmoid(self, xi):
"""our sigmoid function that operates on the hidden layer"""
return 1.0/(1.0 + np.exp(-xi))
def _batch_update(self, x_batch, y_batch):
# batch size
S = len(x_batch)
x = np.array(x_batch).T
y = np.array(y_batch).T
# propagate the input through the network
z_tilde = self.sigmoid(self.B @ x)
z = self.sigmoid(self.A @ z_tilde)
# compute the errors (backpropagate to the hidden layer)
e = z - y
e_tilde = self.A.T @ (e * z * (1 - z))
# corrections
grad_A = (2/S) * e * z * (1 - z) @ z_tilde.T
grad_B = (2/S) * e_tilde * z_tilde * (1 - z_tilde) @ x.T
self.n_trained += S
return grad_A, grad_B
def assess(self):
"""Run through the test data and return the fraction correct
with the currently trained network"""
self.data_manager.reset_testing()
n_correct = 0
while gt := self.data_manager.get_next_test_image():
ans = self.predict(gt)
if gt.validate(ans):
n_correct += 1
return n_correct / self.data_manager.n_test
def train(self, *, n_epochs=1,
learning_rate=0.2, beta_momentum=0.9,
batch_size=64):
"""Train the neural network by doing gradient descent with back
propagation to set the matrix elements in B (the weights
between the input and hidden layer) and A (the weights between
the hidden layer and output layer)
"""
v_A = np.zeros_like(self.A)
v_B = np.zeros_like(self.B)
for i in range(n_epochs):
start = time.perf_counter()
self.data_manager.reset_training()
# storage for our batches
x_batch = []
y_batch = []
while g := self.data_manager.get_next_training_image():
# make a 1-d representation of the input, called x, and call
# the output y
x_batch.append(np.ravel(g.data))
y_batch.append(g.out)
if len(x_batch) == batch_size:
# batch is full -- do the training
grad_A, grad_B = self._batch_update(x_batch, y_batch)
v_A[...] = beta_momentum * v_A + (1.0 - beta_momentum) * grad_A
v_B[...] = beta_momentum * v_B + (1.0 - beta_momentum) * grad_B
self.A[...] += -learning_rate * v_A
self.B[...] += -learning_rate * v_B
x_batch = []
y_batch = []
# we may have run out of data without filling up the
# last batch, so take care of that now
if x_batch:
grad_A, grad_B = self._batch_update(x_batch, y_batch)
v_A[...] = beta_momentum * v_A + (1.0 - beta_momentum) * grad_A
v_B[...] = beta_momentum * v_B + (1.0 - beta_momentum) * grad_B
self.A[...] += -learning_rate * v_A
self.B[...] += -learning_rate * v_B
epoch_time = time.perf_counter() - start
self.training_time += epoch_time
frac_correct = self.assess()
print(f"epoch {i+1:3} | " +
f"test set correct: {frac_correct:5.3f}; " +
f"training time: {epoch_time:7.3f} s")
def predict(self, model):
""" predict the outcome using our trained matrix A """
x_in = np.ravel(model.data)[:, np.newaxis]
y = self.sigmoid(self.A @ (self.sigmoid(self.B @ x_in)))
return y
nn = NeuralNetwork(d, hidden_layer_size=500)
nn.train(n_epochs=100)
epoch 1 | test set correct: 0.143; training time: 41.004 s
epoch 2 | test set correct: 0.201; training time: 41.027 s
epoch 3 | test set correct: 0.205; training time: 40.968 s
epoch 4 | test set correct: 0.213; training time: 40.952 s
epoch 5 | test set correct: 0.221; training time: 41.050 s
epoch 6 | test set correct: 0.279; training time: 41.446 s
epoch 7 | test set correct: 0.280; training time: 39.995 s
epoch 8 | test set correct: 0.286; training time: 40.902 s
epoch 9 | test set correct: 0.295; training time: 41.269 s
epoch 10 | test set correct: 0.335; training time: 41.154 s
epoch 11 | test set correct: 0.346; training time: 51.846 s
epoch 12 | test set correct: 0.358; training time: 51.583 s
epoch 13 | test set correct: 0.378; training time: 51.796 s
epoch 14 | test set correct: 0.370; training time: 51.642 s
epoch 15 | test set correct: 0.374; training time: 53.873 s
epoch 16 | test set correct: 0.390; training time: 53.134 s
epoch 17 | test set correct: 0.365; training time: 53.750 s
epoch 18 | test set correct: 0.375; training time: 51.822 s
epoch 19 | test set correct: 0.406; training time: 54.549 s
epoch 20 | test set correct: 0.402; training time: 52.303 s
epoch 21 | test set correct: 0.390; training time: 56.078 s
epoch 22 | test set correct: 0.399; training time: 51.723 s
epoch 23 | test set correct: 0.429; training time: 53.235 s
epoch 24 | test set correct: 0.417; training time: 55.886 s
epoch 25 | test set correct: 0.426; training time: 52.167 s
epoch 26 | test set correct: 0.395; training time: 53.800 s
epoch 27 | test set correct: 0.433; training time: 52.419 s
epoch 28 | test set correct: 0.437; training time: 50.259 s
epoch 29 | test set correct: 0.457; training time: 52.543 s
epoch 30 | test set correct: 0.437; training time: 53.349 s
epoch 31 | test set correct: 0.440; training time: 51.832 s
epoch 32 | test set correct: 0.458; training time: 53.182 s
epoch 33 | test set correct: 0.463; training time: 53.216 s
epoch 34 | test set correct: 0.483; training time: 55.843 s
epoch 35 | test set correct: 0.476; training time: 51.666 s
epoch 36 | test set correct: 0.488; training time: 52.686 s
epoch 37 | test set correct: 0.496; training time: 54.830 s
epoch 38 | test set correct: 0.476; training time: 53.454 s
epoch 39 | test set correct: 0.480; training time: 52.697 s
epoch 40 | test set correct: 0.490; training time: 57.075 s
epoch 41 | test set correct: 0.484; training time: 52.667 s
epoch 42 | test set correct: 0.504; training time: 55.091 s
epoch 43 | test set correct: 0.486; training time: 53.933 s
epoch 44 | test set correct: 0.497; training time: 55.950 s
epoch 45 | test set correct: 0.508; training time: 52.159 s
epoch 46 | test set correct: 0.527; training time: 52.307 s
epoch 47 | test set correct: 0.519; training time: 51.254 s
epoch 48 | test set correct: 0.506; training time: 53.555 s
epoch 49 | test set correct: 0.534; training time: 53.974 s
epoch 50 | test set correct: 0.516; training time: 51.208 s
epoch 51 | test set correct: 0.498; training time: 54.189 s
epoch 52 | test set correct: 0.530; training time: 50.382 s
epoch 53 | test set correct: 0.521; training time: 40.663 s
epoch 54 | test set correct: 0.513; training time: 41.086 s
epoch 55 | test set correct: 0.526; training time: 40.568 s
epoch 56 | test set correct: 0.542; training time: 40.529 s
epoch 57 | test set correct: 0.543; training time: 40.663 s
epoch 58 | test set correct: 0.544; training time: 40.868 s
epoch 59 | test set correct: 0.551; training time: 40.612 s
epoch 60 | test set correct: 0.544; training time: 40.732 s
epoch 61 | test set correct: 0.546; training time: 40.606 s
epoch 62 | test set correct: 0.561; training time: 40.343 s
epoch 63 | test set correct: 0.539; training time: 40.789 s
epoch 64 | test set correct: 0.552; training time: 41.454 s
epoch 65 | test set correct: 0.545; training time: 40.833 s
epoch 66 | test set correct: 0.562; training time: 40.742 s
epoch 67 | test set correct: 0.551; training time: 40.787 s
epoch 68 | test set correct: 0.549; training time: 40.666 s
epoch 69 | test set correct: 0.544; training time: 40.575 s
epoch 70 | test set correct: 0.559; training time: 40.407 s
epoch 71 | test set correct: 0.563; training time: 40.368 s
epoch 72 | test set correct: 0.568; training time: 40.482 s
epoch 73 | test set correct: 0.573; training time: 40.545 s
epoch 74 | test set correct: 0.554; training time: 40.533 s
epoch 75 | test set correct: 0.582; training time: 40.797 s
epoch 76 | test set correct: 0.589; training time: 41.191 s
epoch 77 | test set correct: 0.587; training time: 41.206 s
epoch 78 | test set correct: 0.568; training time: 41.557 s
epoch 79 | test set correct: 0.588; training time: 40.413 s
epoch 80 | test set correct: 0.585; training time: 40.529 s
epoch 81 | test set correct: 0.592; training time: 40.488 s
epoch 82 | test set correct: 0.593; training time: 40.447 s
epoch 83 | test set correct: 0.575; training time: 40.672 s
epoch 84 | test set correct: 0.599; training time: 40.745 s
epoch 85 | test set correct: 0.582; training time: 40.424 s
epoch 86 | test set correct: 0.611; training time: 40.328 s
epoch 87 | test set correct: 0.581; training time: 40.420 s
epoch 88 | test set correct: 0.599; training time: 40.743 s
epoch 89 | test set correct: 0.599; training time: 40.676 s
epoch 90 | test set correct: 0.607; training time: 40.602 s
epoch 91 | test set correct: 0.578; training time: 40.560 s
epoch 92 | test set correct: 0.601; training time: 40.468 s
epoch 93 | test set correct: 0.586; training time: 40.644 s
epoch 94 | test set correct: 0.618; training time: 40.477 s
epoch 95 | test set correct: 0.608; training time: 40.574 s
epoch 96 | test set correct: 0.578; training time: 40.563 s
epoch 97 | test set correct: 0.604; training time: 40.405 s
epoch 98 | test set correct: 0.582; training time: 40.684 s
epoch 99 | test set correct: 0.610; training time: 40.094 s
epoch 100 | test set correct: 0.590; training time: 40.226 s
Note
We are able to get about 60% correct here, when using the coarsened data. It does appear that more training would help—there are a lot of weights and (relatively) few training images.
Ultimately, a major issue is that the backpropagated errors get really small when using the sigmoid (this is called the vanishing gradient problem). Our network is just too simple for this problem.