Numerical Errors: Roundoff and Truncation

Numerical Errors: Roundoff and Truncation#

We will consider 2 different types of errors:

  • roundoff error: an error arising from how numbers are represented on computers.

  • truncation error: an error that arises from approximations we make in turning math operations (like derivatives) into discrete operations that can be done on a computer.

import matplotlib.pyplot as plt
import numpy as np

Roundoff Error#

Computers use finite amount of memory (64-bits for double precision) to store floating point numbers. This means that we cannot represent the infinite set of numbers in the number line in a finite amount of memory. So most numbers are approximate after a certain number of digits.

Exercise

What is (approximately) the smallest number that can be added to 1 such that the result is still distinct from 1

Hide code cell content 
a = 1.0
eps = 0.1
while a + eps != a:
    eps /= 2.0

# note: eps is now the first value such that 1 + eps is not equal to 1
# so 2*eps is the last value for which they were distinct
print(2*eps)

1.7763568394002506e-16

Math is not associative in floating point. Consider

\[(a + b) + c\]

vs

\[a + (b + c)\]

with \(a =\) 1.0, \(b =\) -1.0, and \(c =\) 2.e-15.

Do these two expressions agree?

a = 1.0
b = -1.0
c = 2.e-15

print((a + b) + c)
print(a + (b + c))

2e-15
1.9984014443252818e-15

Reducing roundoff error#

Often we can reduce roundoff error by changing the order of operations or using algebraically equivalent expressions that have better roundoff properties.

For example, subtracting two very large, nearly identical numbers can result in a loss of precision. Consider:

\[f = a^2 - b^2\]

and the equivalent

\[g = (a - b)(a + b)\]
# the closer together we make these numbers, the larger
# the relative error
a = 1.e18
b = 1.000000001e18

# compute the two algebraically equivalent expressions
f = a**2 - b**2
g = (a - b) * (a + b)

# print both expressions and the relative error
print(f, g, abs((f-g)/g))

-1.9999999769683095e+27 -2.000000001e+27 1.201584528005781e-08

as we make \(a\) and \(b\) closer together, the relative error in the calculation increases.

Exercise

Consider a quadratic equation: \(ax^2 + bx + c\). The two solutions are given by the familiar quadratic equation:

\[x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]

Alternately, we could use the expression:

\[x = \frac{2c}{-b \mp \sqrt{b^2 - 4ac}}\]

For values \(a = 0.001\), \(b = 1000\), and \(c = 0.001\), how do we use these expressions to get the most accurate answer?

(example from Newman)

Hide code cell content 
a = 0.001
b = 1000.0
c = 0.001

# the problem is the sqrt of the discriminant -- it is very
# close to b, so if we subtract it and b, then we maximize
# roundoff error
print(np.sqrt(b**2 - 4*a*c), b)

# we want to choose one solution from each expression --
# the one where there is no cancellation of close numbers
x1 = 2*c/(-b - np.sqrt(b**2 - 4*a*c))
x2 = (-b - np.sqrt(b**2 - 4*a*c))/(2*a)
print(x1, x2)

999.999999998 1000.0
-1.000000000001e-06 -999999.999999

Truncation Error#

Consider Taylor expanding a function \(f(x)\):

\[f(x + h) = f(x) + h f^\prime(x) + \frac{h^2}{2} f^{\prime\prime}(x) + \ldots\]

Rearranging this, we can solve for \(f^\prime(x)\):

\[f^\prime(x) = \frac{f(x+h) - f(x)}{h} - \frac{h}{2} f^{\prime\prime}(x) + \ldots\]

This looks like the definition of a derivative from calculus, but with extra terms that are proportional to \(h\) or higher powers of \(h\).

We can write this as:

\[f^\prime(x) \approx \frac{f(x+h) - f(x)}{h} + \mathcal{O}(h)\]

where \(\mathcal{O}(h)\) here means that the error in this approximation for the derivative is proportion to \(h\). We say this is first-order accurate. This is an example of truncation error – the terms we are ignoring are an error in our approximation.

Exercise

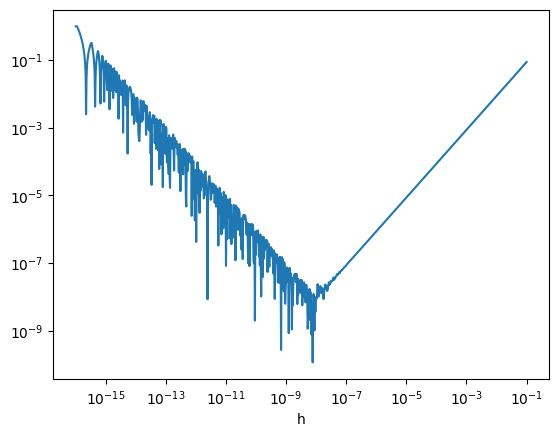
We can explore the relative importance of roundoff and truncation error.
Consider a first-order approximation to the derivative:

\[D_h(x) = \frac{f(x+h) - f(x)}{h}\]

for \(f(x) = \sin(x)\). Plot the error in the approximation, \(D_h(x)\), vs. \(h\). Does it do what you expect?

Hide code cell content 
def f(x):
    """our function to numerically differentiate"""
    return np.sin(x)

def Dh(x, h):
    """a discrete approximation to the derivative at x"""
    return (f(x+h) - f(x))/h

def fprime(x):
    """the analytic derivative of f"""
    return np.cos(x)

# generate a set of h's from 1.e-16 to 0.1
hs = np.logspace(-16, -1, 1000)

# we'll look at the error at pi/3
x = np.pi/3.0

# compute the numerical difference for all h's
num_der = Dh(x, hs)

# get the analytic derivative
ans = fprime(x)

# compute the relative error
err = np.abs(num_der - ans)/ans

# plot the error vs h
fig, ax = plt.subplots()
ax.loglog(hs, err)
ax.set_xlabel("h")

Text(0.5, 0, 'h')
../../_images/4d12fde2f7e09c2bab168919a5e3361947bdd28a9eb8d83a25fc96207250a5bd.png

Let’s discuss the trends:

  • Starting with the largest value of \(h\), as we make \(h\) smaller, we see that the error decreases. This is following the expected behavior of the truncation error derived above.

  • Once our \(h\) becomes really small, roundoff error starts to dominate. In effect, we are seeing that:

    \[(x_0 + h) - x_0 \ne h\]

    because of roundoff error.

  • The minimum error here is around \(\sqrt{\epsilon}\), where \(\epsilon\) is machine epsilon.

Important

Because of roundoff error, we should never exactly compare two floating point numbers, but instead ask they they agree within some tolerance, e.g., test equality as:

\[| x - y | < \epsilon\]

Other Errors#

Overflow#

The finite amount of memory used for storing numbers means that there is a maximum and minimum possible number representable as well.

(credit: xkcd)

NaN and Inf#

These are defined “numbers” that represent floating point errors. Consider:

Some NaNs: \(\sqrt{-1}\), \(0/0\), …

Some infs: \(1/0\)

# the largest exponent we can store in double precision 
# floating point is 308.  What happens if we go beyond that?
a = 1.e308
print(a*10)

inf