Application: Stability of Planetary Systems#
Planetary systems are an example of a few-body problem — each planet exerts a gravitational force on the others, in addition to the dominant gravitation influence of the central star. If the planets get too close, then collisions or ejections can occur.
Hill radius#
An important concept in plantary dynamics is the mutual Hill radius, \(R_h\), which measures how much one planet affects another through their gravitational attraction at closest encounter:
where \(a_1\) and \(a_2\) are the radii of the planet orbits and \(M_1\) and \(M_2\) are their masses (this is closely related to the Hill sphere) and we define the separation between planets 1 and 2 (in circular orbits).
The separation between to planets relative to their hill radius is:
(assuming \(a_2 > a_1\)).
Important
For a system with 2 planets, it turns out that the orbits are stable as long as \(\Delta \gtrsim 3.5\) (see, e.g., Gladman 1993). For more than 2 planets, there is no simple constraint on \(\Delta\), but less massive planets with larger spacings tend to be more stable, and the stability criteria depends on how long you want the system to remain stable (see, e.g., Smith & Lissauer 2009, Morrison & Kratter 2016).
We will attempt to model the stability of a system like HR 8799. A recent investigation of this system was done in Götberg et al. 2016 which found many configurations are unstable to the estimated age of this explanetary system.
import numpy as np
import matplotlib.pyplot as plt
class State:
"""a container to hold an object"""
def __init__(self, mass, x, y, u, v):
self.mass = mass
self.x = x
self.y = y
self.u = u
self.v = v
def __str__(self):
return f"{self.mass:10.6f}: {self.x:10.6f} {self.y:10.6f} {self.u:10.6f} {self.v:10.6f}"
Integrator#
We will implement the 4th order sympletic integrator of Yoshida 1990 (see also Wikipedia’s leapfrong article). This follows the same ideas as the velocity-Verlet method — there is a sequence of drifts and kicks arranged to make the truncation error \(\mathcal{O}(\Delta t^4)\).
Note
We work in units of solar masses, astronomical units, and years.
In setting up our solar system, we require the mass of the star and the semi-major axes and masses of the planets. We will use circular orbits for the planets, with the initial position given a random angle about the Sun (the seed parameter sets the random number generator seed).
Important
We want our system to be at rest and for the barycenter to be at the origin, so once we initialize the planets, we compute the center of mass and momentum and adjust the star’s position and velocity to ensure that the center of mass is at the origin and stationary. This has the side-effect that the planet orbits now have a small initial eccentricity.
Tip
Our integrator will only store the last max_history positions of the planets, since matplotlib can have trouble with really long integration histories. We accomplish this by using a python deque instead of a list to manage
the data.
import collections
Note
We will stop the integration if any of the planets gains a distance from the origin larger than escape_radius.
Close encounters can be problematic. One approach is to switch from using a sympletic integrator to a high-order time-adaptive integrator with error-control once two planets become closer than a few Hill radii (see, e.g., Chatterjee et al. 2008).
Tip
To avoid having to compute the acceleration between a pair of bodies in our solar system twice,
we use itertools.product() to loop give us all pairs of objects and then only compute the force
between them once.
import itertools
class SolarSystem:
"""model the gravitational interaction of a solar system."""
def __init__(self, M_star, *, m_planets=None, a_planets=None,
max_history=50000, SMALL=1.e-30,
seed=1234, escape_radius=10000):
# initialize the random number generator
np.random.seed(seed)
# Yoshida integrator constants
cbrt2 = np.cbrt(2)
w0 = -cbrt2 / (2 - cbrt2)
w1 = 1 / (2 - cbrt2)
self.c = np.array([w1 / 2, 0.5 * (w0 + w1), 0.5 * (w0 + w1), w1 / 2])
self.d = np.array([w1, w0, w1])
self.G = 4 * np.pi**2 # units AU**3 / (solar mass * year**2)
self.M_star = M_star
self.escape_radius = escape_radius
self.a_initial = [0] + a_planets
# store the history of the solar system
self.history = collections.deque(maxlen=max_history)
# we have the star and planets
self.nobjects = len(m_planets) + 1
# current solar system
system = []
# store the star
system.append(State(M_star, 0.0, 0.0, 0.0, 0.0))
# store the planets
assert len(m_planets) == len(a_planets)
for m, a in zip(m_planets, a_planets):
# pick a random angle and then set the velocity to be circular
phi = np.random.uniform(0, 2.0*np.pi)
v_circ = np.sqrt(self.G * self.M_star / a)
system.append(State(m,
a*np.cos(phi), a*np.sin(phi),
-v_circ*np.sin(phi), v_circ*np.cos(phi)))
# now correct the star's state so the center of mass is stationary
# and at the origin
system[0].x = -sum(s.mass * s.x for n, s in enumerate(system) if n != 0) / M_star
system[0].y = -sum(s.mass * s.y for n, s in enumerate(system) if n != 0) / M_star
system[0].u = -sum(s.mass * s.u for n, s in enumerate(system) if n != 0) / M_star
system[0].v = -sum(s.mass * s.v for n, s in enumerate(system) if n != 0) / M_star
# store the initial state
self.history.append(system)
self.SMALL = SMALL
self.time = collections.deque([0.0], maxlen=max_history)
h = self.compute_hill_separation(system)
print(f"initial minimum relative separation / Hill radius = {h.min()}")
def npts(self):
"""return the number of integration points"""
return len(self.time)
def compute_hill_separation(self, state):
"""compute the multiual Hill radius for each pair of planets"""
h_sep = np.zeros((self.nobjects, self.nobjects))
h_sep[:, :] = np.inf
# loop over the pairs of planets
for p1, p2 in itertools.product(range(1, self.nobjects),
range(1, self.nobjects)):
if p1 >= p2:
continue
a1 = np.sqrt((state[p1].x - state[0].x)**2 +
(state[p1].y - state[0].y)**2)
a2 = np.sqrt((state[p2].x - state[0].x)**2 +
(state[p2].y - state[0].y)**2)
r_hill = 0.5 * (a1 + a2) * np.cbrt((state[p1].mass +
state[p2].mass) /
(3 * self.M_star))
h_sep[p1, p2] = np.abs(a2 - a1) / r_hill
h_sep[p2, p1] = h_sep[p1, p2]
return h_sep
def rhs(self, states):
"""states is (State, State, ...)"""
ydots = []
# first setup the State objects for each body
# with only dx/dt and dy/dt initialized
for s in states:
ydots.append(State(s.mass, s.u, s.v, 0, 0))
# now loop over all unique pairs of objects and add
# to the acceleration that each object in the pair feels
for iobj, jobj in itertools.product(range(self.nobjects),
range(self.nobjects)):
if iobj >= jobj:
continue
dx = states[jobj].x - states[iobj].x
dy = states[jobj].y - states[iobj].y
r = np.sqrt(dx**2 + dy**2) + self.SMALL
ax = self.G * dx / r**3
ay = self.G * dy / r**3
ydots[iobj].u += states[jobj].mass * ax
ydots[iobj].v += states[jobj].mass * ay
ydots[jobj].u += -states[iobj].mass * ax
ydots[jobj].v += -states[iobj].mass * ay
return ydots
def single_step_yoshida(self, states_old, dt):
"""take a single step using the 4th order Yoshida integrator"""
# we can just work on the "new" state directly, so start by
# copying the old to new
states_new = []
for s in states_old:
states_new.append(State(s.mass, s.x, s.y, s.u, s.v))
# drift with current velocity
for s in states_new:
s.x += self.c[0] * s.u * dt
s.y += self.c[0] * s.v * dt
for i in range(3):
# evaluate the force
ydots = self.rhs(states_new)
# kick followed by drift
for n, s in enumerate(states_new):
s.u += self.d[i] * ydots[n].u * dt
s.v += self.d[i] * ydots[n].v * dt
s.x += self.c[i+1] * s.u * dt
s.y += self.c[i+1] * s.v * dt
return states_new
def integrate(self, dt, tmax):
"""integrate our system"""
t = self.time[-1]
escaped = False
while t < tmax and not escaped:
dt = min(dt, tmax-t)
states_old = self.history[-1]
states_new = self.single_step_yoshida(states_old, dt)
t += dt
self.time.append(t)
self.history.append(states_new)
# check if any planet has escaped
for n, s in enumerate(states_new):
if n == 0:
continue
if np.sqrt(s.x**2 + s.y**2) > self.escape_radius:
print(f"planet {n} escaped!")
escaped = True
def plot(self, draw_original_orbits=True):
fig, ax = plt.subplots()
if draw_original_orbits:
theta = np.radians(np.arange(361))
for n in range(self.nobjects):
ax.plot(self.a_initial[n]*np.cos(theta),
self.a_initial[n]*np.sin(theta),
ls=":", color=f"C{n}")
for n in range(self.nobjects):
xs = [q[n].x for q in self.history]
ys = [q[n].y for q in self.history]
if n == 0:
label = "*"
else:
label = f"planet {n}"
ax.plot(xs, ys, color=f"C{n}", label=label)
ax.axis("equal")
ax.legend(fontsize="small")
return fig
First integration test#
We’ll start with only 3 planets in the system. These are picked such that the initial \(\Delta > 3\) for the system.
# the system seems stable if we omit planet 3
m_planets = [0.0054, 0.0074, 0.0071]
a_planets = [71.6, 41.4, 16.3]
s = SolarSystem(1.5, m_planets=m_planets, a_planets=a_planets,
escape_radius=1000)
initial minimum relative separation / Hill radius = 3.778998530885095
for o in s.history[0]:
print(o)
1.500000: 0.125746 -0.128205 0.002400 0.011411
0.005400: 25.720964 66.820596 -0.848724 0.326696
0.007400: -29.801160 -28.737621 0.830187 -0.860911
0.007100: -15.068147 6.216185 -0.726889 -1.761992
s.integrate(0.05, 50000)
fig = s.plot()
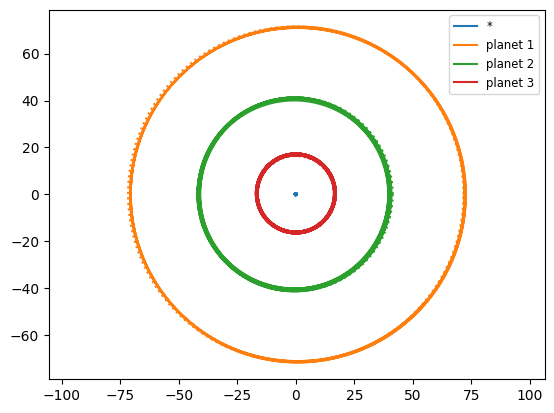
HR 8799 analogue#
Now we’ll add the 4th planet, giving us a system that approximates HR 8799.
# these are roughly the HR 8799 planet orbits
m_planets = [0.0054, 0.0074, 0.0087, 0.0071]
a_planets = [71.6, 41.4, 26.7, 16.3]
s = SolarSystem(1.5, m_planets=m_planets, a_planets=a_planets,
escape_radius=1000)
s.integrate(0.05, 50000)
fig = s.plot()
initial minimum relative separation / Hill radius = 2.787501730226769
planet 4 escaped!
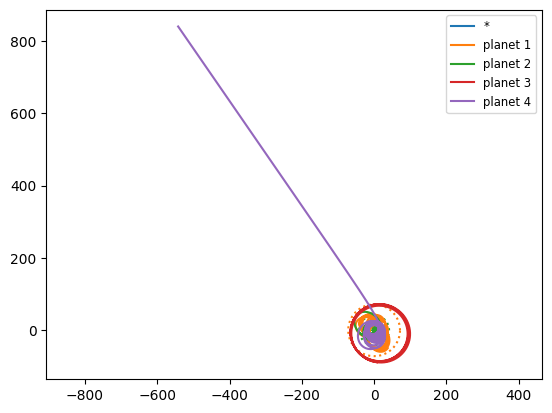
We can try different seeds, but the systems seem to always become unstable
s = SolarSystem(1.5, m_planets=m_planets, a_planets=a_planets,
escape_radius=1000, seed=1)
s.integrate(0.05, 50000)
fig = s.plot()
initial minimum relative separation / Hill radius = 2.8570026966331477
planet 3 escaped!
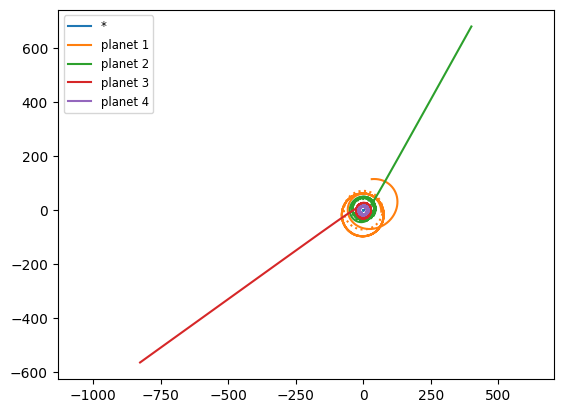
Increasing the spacing#
Let’s try with the same number of planets and masses, but we’ll increase the spacing a bit
m_planets = [0.0054, 0.0074, 0.0087, 0.0071]
a_planets = [80, 45, 25, 15]
s = SolarSystem(1.5, m_planets=m_planets, a_planets=a_planets,
escape_radius=1000)
s.integrate(0.05, 50000)
fig = s.plot()
initial minimum relative separation / Hill radius = 3.3947859294168876
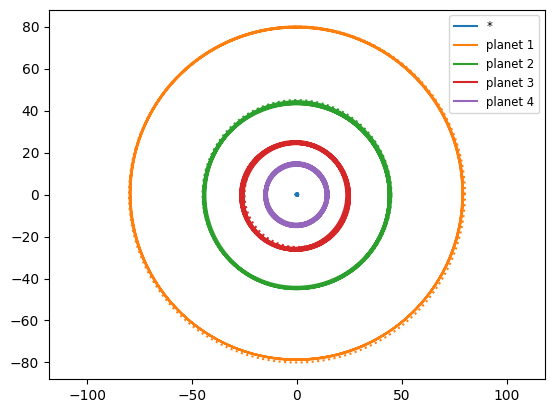
C++ implementation#
The C++ implementation is available as:
-
#ifndef ORBIT_STATE_H #define ORBIT_STATE_H #include <iostream> #include <iomanip> struct OrbitState { // a container to hold the star positions double mass{}; double x{}; double y{}; double u{}; double v{}; OrbitState(double M, double x0, double y0, double u0, double v0) : mass(M), x(x0), y(y0), u(u0), v(v0) {} OrbitState() {} }; inline std::ostream& operator<< (std::ostream& os, const OrbitState& s) { os.precision(6); os << std::setw(14) << s.mass << std::setw(14) << s.x << std::setw(14) << s.y << std::setw(14) << s.u << std::setw(14) << s.v; return os; } #endif
-
#ifndef SOLAR_SYSTEM_H #define SOLAR_SYSTEM_H #include <algorithm> #include <array> #include <cassert> #include <cmath> #include <cstddef> #include <deque> #include <iterator> #include <limits> #include <random> #include <vector> #include "orbit_state.H" constexpr double G_const{4.0 * M_PI * M_PI}; class SolarSystem { double M_star{}; double escape_R{}; // Yoshida integration constants std::array<double, 4> c{}; std::array<double, 3> d{}; public: // for plotting, we'll store all the initial semi-major // axes, including the star's std::vector<double> a_initial; std::deque<std::vector<OrbitState>> history; std::deque<double> times; int n_objects{}; const double SMALL{1.e-30}; SolarSystem(double M_in, const std::vector<double>& m_planets, const std::vector<double>& a_planets, double escape_radius=10000) : M_star(M_in), escape_R(escape_radius) { assert (m_planets.size() == a_planets.size()); // integration constants const double w0 = -std::cbrt(2.0) / (2.0 - cbrt(2.0)); const double w1 = 1.0 / (2.0 - std::cbrt(2.0)); c[0] = w1 / 2.0; c[1] = 0.5 * (w0 + w1); c[2] = c[1]; c[3] = c[0]; d[0] = w1; d[1] = w0; d[2] = w1; a_initial.push_back(0.0); std::copy(a_planets.cbegin(), a_planets.cend(), std::back_inserter(a_initial)); n_objects = a_initial.size(); // create the initial solar system std::vector<OrbitState> system; // store the star system.emplace_back(M_star, 0.0, 0.0, 0.0, 0.0); // now the planets. We will give them random phases // seed the random number generator std::mt19937 generator(123); std::uniform_real_distribution<double> uniform(0.0, 1.0); for (std::size_t n = 0; n < m_planets.size(); ++n) { double phi = uniform(generator) * 2.0 * M_PI; double v_circ = std::sqrt(G_const * M_star / a_planets[n]); system.emplace_back(m_planets[n], a_planets[n] * std::cos(phi), a_planets[n] * std::sin(phi), -v_circ * std::sin(phi), v_circ * std::cos(phi)); } // now correct the star's state so the center of mass // is stationary and at the origin // note: since the star was initialized with all 0s, // we can include it in the sum here without issue double mx_sum{}; double my_sum{}; double mu_sum{}; double mv_sum{}; for (const auto& object : system) { mx_sum += object.mass * object.x; my_sum += object.mass * object.y; mu_sum += object.mass * object.u; mv_sum += object.mass * object.v; }; system[0].x -= mx_sum / system[0].mass; system[0].y -= my_sum / system[0].mass; system[0].u -= mu_sum / system[0].mass; system[0].v -= mv_sum / system[0].mass; // store the initial conditions history.push_back(system); times.push_back(0.0); } double compute_hill_separation(const std::vector<OrbitState>& state) { double h_sep{std::numeric_limits<double>::max()}; for (int p1 = 1; p1 < n_objects; ++p1) { double a1 = std::sqrt(std::pow(state[p1].x - state[0].x, 2) + std::pow(state[p1].y - state[0].y, 2)); // only consider unique pairs of p1 and p2 for (int p2 = 1; p2 < p1; ++p2) { double a2 = std::sqrt(std::pow(state[p2].x - state[0].x, 2) + std::pow(state[p2].y - state[0].y, 2)); double r_hill = 0.5 * (a1 + a2) * std::cbrt((state[p1].mass + state[p2].mass) / (3.0 * M_star)); h_sep = std::min(h_sep, std::abs(a2 - a1) / r_hill); } } return h_sep; } std::vector<OrbitState> rhs(const std::vector<OrbitState>& states) { std::vector<OrbitState> ydots; for (int iobj = 0; iobj < n_objects; ++iobj) { ydots.emplace_back(states[iobj].mass, states[iobj].u, states[iobj].v, 0.0, 0.0); } // now loop over unique pairs and compute the force between // the two objects and add to both their accelerations for (int iobj = 0; iobj < n_objects; ++iobj) { for (int jobj = 0; jobj < iobj; ++jobj) { double dx = states[jobj].x - states[iobj].x; double dy = states[jobj].y - states[iobj].y; double r = std::sqrt(dx * dx + dy * dy + SMALL); double ax = G_const * dx / (r * r * r); double ay = G_const * dy / (r * r * r); ydots[iobj].u += states[jobj].mass * ax; ydots[iobj].v += states[jobj].mass * ay; ydots[jobj].u += -states[iobj].mass * ax; ydots[jobj].v += -states[iobj].mass * ay; } } return ydots; } std::vector<OrbitState> single_step_yoshida(const std::vector<OrbitState>& states, const double dt) { // we can just work on the new state directly, so start by simply // copying the old state to the new state std::vector<OrbitState> states_new; std::copy(states.cbegin(), states.cend(), std::back_inserter(states_new)); // drift with the current velocity for (auto& s : states_new) { s.x += c[0] * s.u * dt; s.y += c[0] * s.v * dt; } for (int i = 0; i < 3; ++i) { // evaluate the force auto ydots = rhs(states_new); for (int n = 0; n < n_objects; ++n) { states_new[n].u += d[i] * ydots[n].u * dt; states_new[n].v += d[i] * ydots[n].v * dt; states_new[n].x += c[i+1] * states_new[n].u * dt; states_new[n].y += c[i+1] * states_new[n].v * dt; } } return states_new; } void integrate(const double dt_in, const double tmax) { auto t = times.back(); bool escaped{false}; double dt{dt_in}; while (t < tmax && ! escaped) { const auto& states_old = history.back(); dt = std::min(dt, tmax-t); auto states_new = single_step_yoshida(states_old, dt); t += dt; times.push_back(t); history.push_back(states_new); // check if any planet has escaped for (int n = 1; n < n_objects; ++n) { double r = std::sqrt(std::pow(states_new[n].x, 2) + std::pow(states_new[n].x, 2)); if (r > escape_R) { escaped = true; break; } } } } }; #endif
-
#include <fstream> #include <iomanip> #include <iostream> #include <vector> #include "solar_system.H" int main() { std::vector<double> m_planets{0.0054, 0.0074, 0.0071}; std::vector<double> a_planets{71.6, 41.4, 16.3}; SolarSystem s(1.5, m_planets, a_planets, 1000); for (const auto& states : s.history) { for (const auto& o : states) { std::cout << o << std::endl; } } std::cout << "initial hill separation = " << s.compute_hill_separation(s.history[0]) << std::endl; s.integrate(0.05, 50000); std::ofstream of("planetary_stability.dat"); for (std::size_t n = 0; n < s.history.size(); ++n) { const auto& states = s.history[n]; of << std::setw(14) << s.times[n]; for (const auto& object : states) { of << object; } of << std::endl; } }


