Application: Galaxy Classification with Keras#
Now we’ll try to do the galaxy classification with Keras. This will allow us to explore more features in the network.
In particular we’ll use a convolutional neural network.
import numpy as np
import matplotlib.pyplot as plt
import h5py
We’ll need the Galaxy class we defined earlier.
galaxy_types = {0: "disturbed galaxies",
1: "merging galaxies",
2: "round smooth galaxies",
3: "in-between round smooth galaxies",
4: "cigar shaped smooth galaxies",
5: "barred spiral galaxies",
6: "unbarred tight spiral galaxies",
7: "unbarred loose spiral galaxies",
8: "edge-on galaxies without bulge",
9: "edge-on galaxies with bulge"}
class Galaxy:
def __init__(self, data, answer, *, index=-1):
self.data = np.array(data, dtype=np.float32) / 255.0
self.answer = answer
self.index = index
def plot(self, ax=None):
if ax is None:
fig, ax = plt.subplots()
ax.imshow(self.data, interpolation="nearest")
ax.text(0.025, 0.95, f"answer: {self.answer}",
color="white", transform=ax.transAxes)
def validate(self, prediction):
"""check if a categorical prediction matches the answer"""
return np.argmax(prediction) == self.answer
A data manager class#
We’ll create a class to manage access to the data. This is similar to the version in our “from scratch” implementation, except we do the batching in the generator. This will do the following:
open the file and store the handles to access the data
partition the data into test and training sets
allow for transformations (rotation, flipping)
provide a means to shuffle the data
provide a generator to get the next batch of training data
allow us to coarsen the images to a reduced resolution to make the training easier.
Tip
We will read all of the data once, which will take about 3.5 GB of memory. It is kept
as a uint8 until needed.
from keras.utils import to_categorical
class DataManager:
def __init__(self, partition=0.8,
batch_size=32,
n_transforms=1,
datafile="Galaxy10_DECals.h5",
coarsen=1):
"""manage access to the data
partition: fraction that should be training
datafile: name of the hdf5 file with the data
coarsen: reduce the number of pixels by this factor
"""
self.ds = h5py.File(datafile)
self.ans = np.array(self.ds["ans"])
self.images = np.array(self.ds["images"])
self.coarsen = coarsen
self.n_transforms = n_transforms
self.batch_size = batch_size
N = len(self.ans)
# create a set of indices for the galaxies and randomize
self.indices = np.arange(N, dtype=np.uint32)
self.rng = np.random.default_rng()
self.rng.shuffle(self.indices)
# partition into training and test sets
# these indices will always refer to the index in the original
# unsplit dataset
n_cut = int(partition * N)
# we want this to be a multiple of the batch size
n_cut -= n_cut % self.batch_size
self.training_indices = self.indices[0:n_cut]
self.test_indices = self.indices[n_cut:N]
self.n_training = len(self.training_indices)
self.n_test = len(self.test_indices)
# number of batches for the training
self.n_batches = n_cut // self.batch_size
self.n_batches *= (n_transforms + 1)
# shape information
self.input_shape = self._get_galaxy(0).data.shape
def _get_galaxy(self, index):
"""return a numpy array containing a single galaxy image, coarsened
if necessary by averaging"""
_tmp = self.images[index, :, :, :]
if self.coarsen > 1:
_tmp = np.mean(_tmp.reshape(_tmp.shape[0]//self.coarsen, self.coarsen,
_tmp.shape[1]//self.coarsen, self.coarsen,
_tmp.shape[2]), axis=(1, 3))
return _tmp
def training_images(self):
self.reset_training()
for idx in self.training_indices:
yield Galaxy(self._get_galaxy(idx), self.ans[idx], index=idx)
def batched_training_generator(self):
while True:
self.reset_training()
batch_x = []
batch_y = []
for idx in self.training_indices:
g = Galaxy(self._get_galaxy(idx), self.ans[idx], index=idx)
batch_x.append(g.data)
batch_y.append(to_categorical(g.answer, 10))
if self.n_transforms > 0:
# rotation
batch_x.append(np.rot90(g.data, axes=(0, 1)))
batch_y.append(to_categorical(g.answer, 10))
if self.n_transforms > 1:
# flipping first axis
batch_x.append(g.data[::-1, :, :])
batch_y.append(to_categorical(g.answer, 10))
if self.n_transforms > 2:
# flipping second axis
batch_x.append(g.data[:, ::-1, :])
batch_y.append(to_categorical(g.answer, 10))
if len(batch_x) == self.batch_size:
yield (np.array(batch_x), np.array(batch_y))
batch_x = []
batch_y = []
def reset_training(self):
"""prepare for the next epoch: shuffle the training data and
reset the index to point to the start"""
self.rng.shuffle(self.training_indices)
def testing_images(self):
for idx in self.test_indices:
yield Galaxy(self._get_galaxy(idx), self.ans[idx], index=idx)
Tip
The training_images() and testing_images() are generators (like range()), so we can iterate like:
d = DataManager()
for g in d.training_images():
# do stuff with g
and g is only converted to 32-bit float as needed.
Here we create a DataManager that will coarsen the images by a factor of 2 (so they will be 128x128 pixels with 3 colors).
We also need to specify the batch size.
d = DataManager(coarsen=2, batch_size=128)
for n, (x, y) in enumerate(d.batched_training_generator()):
print(x.shape)
break
(128, 128, 128, 3)
d.input_shape
(128, 128, 3)
we can see how many images there are in the training and test sets
d.n_training, d.n_test
(14080, 3656)
d.n_batches
220
We can then get loop over training galaxies and look at them (we’ll break after 5):
for n, g in enumerate(d.training_images()):
g.plot()
if n == 4:
break


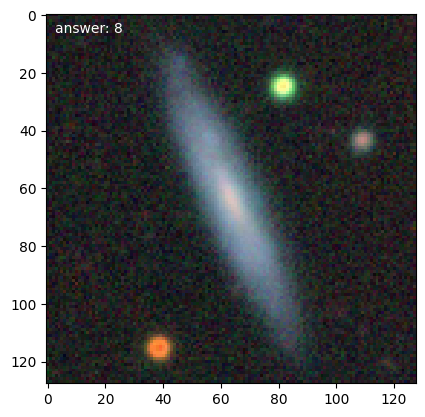


Note
Each time we access the generator it randomizes the galaxies in the training set.
Implementing our neural network#
We’ll use just a single hidden layer. If we use more hidden layers, then there are so many parameters that we will need to do a lot of training (epochs).
Tip
Our DataManager will tell us the size of the input layer, the number of batches, the batch size, etc.
from keras.models import Sequential
from keras.layers import Input, Dense, Dropout, Conv2D, MaxPooling2D, Flatten
model = Sequential()
model.add(Input(shape=d.input_shape))
model.add(Conv2D(32, kernel_size=(3, 3), activation="relu"))
model.add(Conv2D(32, kernel_size=(3, 3), activation="relu"))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Conv2D(64, kernel_size=(3, 3), activation="relu"))
model.add(Conv2D(64, kernel_size=(3, 3), activation="relu"))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Conv2D(128, kernel_size=(3, 3), activation="relu"))
model.add(Conv2D(128, kernel_size=(3, 3), activation="relu"))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Flatten())
model.add(Dense(10, activation="softmax"))
model.summary()
Model: "sequential"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ conv2d (Conv2D) │ (None, 126, 126, 32) │ 896 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ conv2d_1 (Conv2D) │ (None, 124, 124, 32) │ 9,248 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ max_pooling2d (MaxPooling2D) │ (None, 62, 62, 32) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ conv2d_2 (Conv2D) │ (None, 60, 60, 64) │ 18,496 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ conv2d_3 (Conv2D) │ (None, 58, 58, 64) │ 36,928 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ max_pooling2d_1 (MaxPooling2D) │ (None, 29, 29, 64) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ conv2d_4 (Conv2D) │ (None, 27, 27, 128) │ 73,856 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ conv2d_5 (Conv2D) │ (None, 25, 25, 128) │ 147,584 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ max_pooling2d_2 (MaxPooling2D) │ (None, 12, 12, 128) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ flatten (Flatten) │ (None, 18432) │ 0 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense (Dense) │ (None, 10) │ 184,330 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 471,338 (1.80 MB)
Trainable params: 471,338 (1.80 MB)
Non-trainable params: 0 (0.00 B)
We’ll use a different optimizer now, the Adam optimizer. This is supposed to be one of the best that Keras provides.
from keras.optimizers import Adam
rms = Adam()
model.compile(loss='categorical_crossentropy',
optimizer=rms, metrics=['accuracy'])
The keras fit() method can work with a generator directly, so we just pass in the generator.
model.fit(d.batched_training_generator(),
batch_size=d.batch_size,
steps_per_epoch=d.n_batches,
epochs=25)
Epoch 1/25
220/220 ━━━━━━━━━━━━━━━━━━━━ 314s 1s/step - accuracy: 0.2580 - loss: 1.9696
Epoch 2/25
220/220 ━━━━━━━━━━━━━━━━━━━━ 314s 1s/step - accuracy: 0.5889 - loss: 1.1920
Epoch 3/25
220/220 ━━━━━━━━━━━━━━━━━━━━ 317s 1s/step - accuracy: 0.7057 - loss: 0.8792
Epoch 4/25
220/220 ━━━━━━━━━━━━━━━━━━━━ 380s 2s/step - accuracy: 0.7686 - loss: 0.6837
Epoch 5/25
220/220 ━━━━━━━━━━━━━━━━━━━━ 330s 2s/step - accuracy: 0.8089 - loss: 0.5588
Epoch 6/25
220/220 ━━━━━━━━━━━━━━━━━━━━ 326s 1s/step - accuracy: 0.8374 - loss: 0.4862
Epoch 7/25
220/220 ━━━━━━━━━━━━━━━━━━━━ 328s 1s/step - accuracy: 0.8750 - loss: 0.3714
Epoch 8/25
220/220 ━━━━━━━━━━━━━━━━━━━━ 328s 1s/step - accuracy: 0.9020 - loss: 0.2928
Epoch 9/25
220/220 ━━━━━━━━━━━━━━━━━━━━ 326s 1s/step - accuracy: 0.9249 - loss: 0.2189
Epoch 10/25
220/220 ━━━━━━━━━━━━━━━━━━━━ 332s 2s/step - accuracy: 0.9411 - loss: 0.1760
Epoch 11/25
220/220 ━━━━━━━━━━━━━━━━━━━━ 332s 2s/step - accuracy: 0.9582 - loss: 0.1278
Epoch 12/25
220/220 ━━━━━━━━━━━━━━━━━━━━ 327s 1s/step - accuracy: 0.9620 - loss: 0.1190
Epoch 13/25
220/220 ━━━━━━━━━━━━━━━━━━━━ 317s 1s/step - accuracy: 0.9633 - loss: 0.1192
Epoch 14/25
220/220 ━━━━━━━━━━━━━━━━━━━━ 314s 1s/step - accuracy: 0.9682 - loss: 0.1072
Epoch 15/25
220/220 ━━━━━━━━━━━━━━━━━━━━ 317s 1s/step - accuracy: 0.9754 - loss: 0.0870
Epoch 16/25
220/220 ━━━━━━━━━━━━━━━━━━━━ 314s 1s/step - accuracy: 0.9747 - loss: 0.0900
Epoch 17/25
220/220 ━━━━━━━━━━━━━━━━━━━━ 315s 1s/step - accuracy: 0.9804 - loss: 0.0758
Epoch 18/25
220/220 ━━━━━━━━━━━━━━━━━━━━ 321s 1s/step - accuracy: 0.9772 - loss: 0.0734
Epoch 19/25
220/220 ━━━━━━━━━━━━━━━━━━━━ 314s 1s/step - accuracy: 0.9827 - loss: 0.0693
Epoch 20/25
220/220 ━━━━━━━━━━━━━━━━━━━━ 322s 1s/step - accuracy: 0.9815 - loss: 0.0677
Epoch 21/25
220/220 ━━━━━━━━━━━━━━━━━━━━ 311s 1s/step - accuracy: 0.9827 - loss: 0.0591
Epoch 22/25
220/220 ━━━━━━━━━━━━━━━━━━━━ 304s 1s/step - accuracy: 0.9828 - loss: 0.0646
Epoch 23/25
220/220 ━━━━━━━━━━━━━━━━━━━━ 303s 1s/step - accuracy: 0.9853 - loss: 0.0575
Epoch 24/25
220/220 ━━━━━━━━━━━━━━━━━━━━ 302s 1s/step - accuracy: 0.9864 - loss: 0.0511
Epoch 25/25
220/220 ━━━━━━━━━━━━━━━━━━━━ 303s 1s/step - accuracy: 0.9897 - loss: 0.0512
<keras.src.callbacks.history.History at 0x7f8536f946e0>
Assessing#
Now try the test set that the training did not see
n_correct = 0
for g in d.testing_images():
res = model.predict(np.expand_dims(g.data, axis=0), verbose=0)
if np.argmax(res) == g.answer:
n_correct += 1
print(f"fraction correct = {n_correct / d.n_test}")
fraction correct = 0.7097921225382933
We see that we are getting about 70% of the galaxies we didn’t train on correct.


