Application: Reaction Rate Temperature Sensitivity

Stars are powered by nuclear fusion—combining light nuclei into heavier nuclei and releasing binding energy in the process. Reaction rates have complex temperature dependences. For example, the 3-\(\alpha\) reaction rate (capturing \({}^4\mathrm{He} + {}^4\mathrm{He} + {}^4\mathrm{He} \rightarrow {}^{12}\mathrm{C}\)) appears as:

\[q_{3\alpha} = 5.09\times 10^{11} \rho^2 Y^3 T_8^{-3} e^{-44.027/T8}~\mathrm{erg~g^{-1}~s^{-1}}\]

where \(\rho\) is density, \(Y\) is the mass fraction of He, and \(T_8 = T / (10^8~\mathrm{K})\), with \(T\) the temperature.

Reaction vs. temperature

Let’s visualize how this appears as a function of temperature.

import matplotlib.pyplot as plt
import numpy as np

def q3a(T):
    """this is the triple alpha reaction rate / rho^2 Y^3"""
    T8 = T/1e8
    return 5.09e11 * T8**-3 * np.exp(-44.027/T8)

fig, ax = plt.subplots()
T = np.logspace(np.log10(3.e8), np.log10(5.e9), 100)

ax.loglog(T, q3a(T))
ax.set_xlabel("T (K)")
ax.set_ylabel(r"$q_{3\alpha}/(\rho^2 Y^3)$")
ax.grid(ls=":")

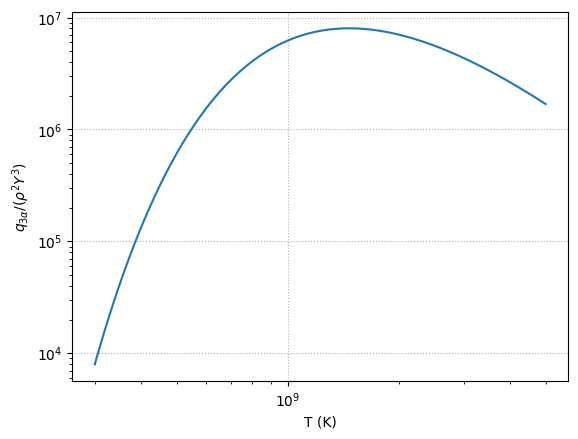
Powerlaw approximation

Often, we want a simpler expression for the energy generation rate, as a powerlaw:

\[q_{3\alpha} = q_0 \rho^2 Y^3 \left (\frac{T}{T_0} \right )^\nu\]

around a temperature \(T_0\).

Here, \(\nu\), is the temperature exponent of the rate, and tells us how sensitive the reactions are to changes in temperature. We see that:

\[\nu = \left . \frac{d\log q}{d\log T}\right |_{T_0} = \left ( \frac{T}{q} \frac{dq}{dT} \right )_{T_0}\]

From the plot, we can see that the slope changes a lot, so \(\nu\) will vary quite a bit depending on our choice of \(T_0\).

We can compute this via numerical differencing. Based on our understand of roundoff and truncation error, we’ll perturb the temperature by \(10^{-8}\).

print("   T        nu")
for T0 in [1.e8, 2.5e8, 5.e8, 1.e9, 2.5e9, 5e9]:
    dT = 1.e-8 * T0
    nu = (T0/q3a(T0)) * (q3a(T0 + dT) - q3a(T0))/dT
    print(f"{T0:8.5g} : {nu:5.2f}")

   T        nu
   1e+08 : 41.03
 2.5e+08 : 14.61
   5e+08 :  5.81
   1e+09 :  1.40
 2.5e+09 : -1.24
   5e+09 : -2.12

We see that at a temperature of \(10^8~\mathrm{K}\), the 3-\(\alpha\) rate is \(\sim T^{40}\)!

C++ implementation

Here’s the same code in C++: 3alpha.cpp

Note

Because of the use of std::println(), this needs to be compiled with C++23, e.g.,

g++ -std=c++23 -o 3alpha 3alpha.cpp

#include <iostream>
#include <cmath>
#include <print>

// compute the triple alpha reaction rate / rho^2 Y^3
double q3a(const double T) {
    double T8{T/1.e8};
    return 5.09e11 * std::pow(T8, -3.0) * std::exp(-44.027/T8);
}

int main() {

    for (auto T0 : {1.e8, 2.5e8, 5.e8, 1.e9, 2.5e9, 5e9}) {
        double dT{1.e-8 * T0};
        double nu = (T0 / q3a(T0)) * (q3a(T0 + dT) - q3a(T0)) / dT;

        std::println("{:8.5g} : {:5.2f}", T0, nu);
    }
}