V-Cycles

We now have what we need to apply this two-grid solver recursively. Instead of solving the coarse grid directly via smoothing, we instead treat it like a new Poisson problem to solve and create an even coarser grid to do the correction, and so on…

Eventually, we will have a tower of grids spanning from our original fine grid resolution down to something suitably coarse that we can relax the solution there with only a few iterations:

To make things simpler, we’ll work with grids that are a power of 2 in size. Then we will coarsen all the way down until we have a grid with only 2 zones (because of how we implement our boundary conditions, we can’t go all the way down to a single zone).

On that 2 zone coarsest grid, just a few smoothing iterations will solve the problem. We call this the bottom solver.

Here’s a multigrid class that implements this recursive structure. It is currently implemented only for homogeneous boundary conditions.

The main data structure is a list of grids, Multigrid.grids, which holds the hierarchy of grids at the different resolutions.

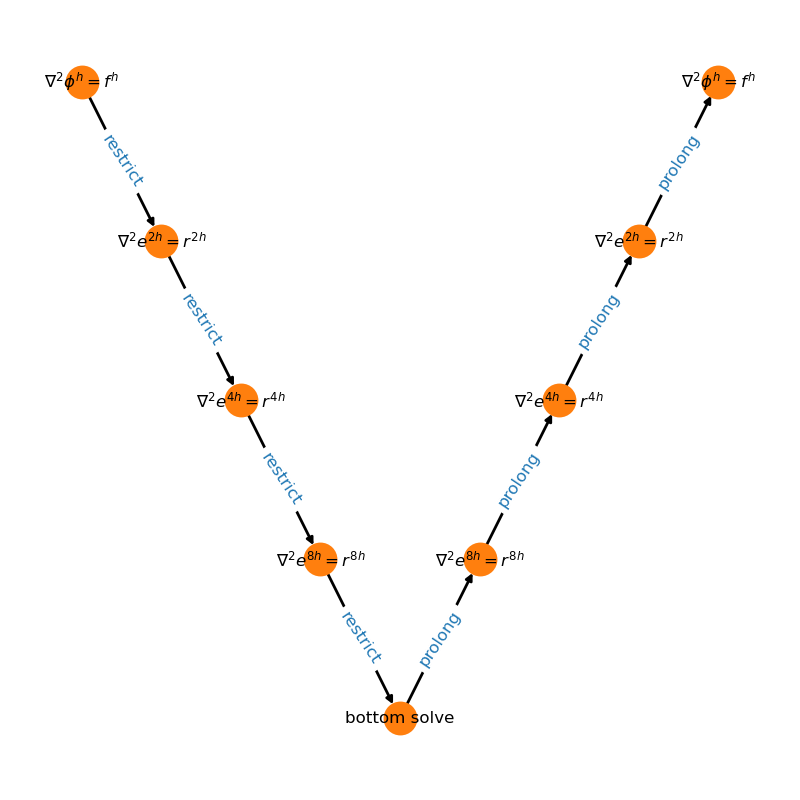
Our two-grid correction code that we previously implemented is now called vcycle(), and it will apply the two-grid correction on all grids except the very coarsest, on which it instead just smooths.

Finally, there is one new function here, solve(). This calls vcycle() repeatedly until the error is below our desired tolerance.

The overall flow looks like:

import numpy as np
import matplotlib.pyplot as plt

import multigrid

%cat multigrid.py

import numpy as np

import grid


class Multigrid:
    """
    The main multigrid class for cell-centered data.

    We require that nx be a power of 2 for simplicity
    """

    def __init__(self, nx, xmin=0.0, xmax=1.0,
                 bc_left_type="dirichlet", bc_right_type="dirichlet",
                 nsmooth=10, nsmooth_bottom=50,
                 verbose=0,
                 true_function=None):

        self.nx = nx
        self.ng = 1

        self.xmin = xmin
        self.xmax = xmax

        self.nsmooth = nsmooth
        self.nsmooth_bottom = nsmooth_bottom

        self.max_cycles = 100

        self.verbose = verbose

        self.bc_left_type = bc_left_type
        self.bc_right_type = bc_right_type

        # a function that gives the analytic solution (if available)
        # for diagnostics only
        self.true_function = true_function

        # assume that self.nx = 2^(nlevels-1)
        # this defines nlevels such that we end exactly on a 2 zone grid
        self.nlevels = int(np.log(self.nx)/np.log(2.0))

        # a multigrid object will be a list of grids
        self.grids = []

        # create the grids.  Here, self.grids[0] will be the coarsest
        # grid and self.grids[nlevel-1] will be the finest grid we
        # store the solution, v, the rhs, f.

        nx_t = 2
        for _ in range(self.nlevels):

            # add a grid for this level
            self.grids.append(grid.Grid(nx_t, xmin=self.xmin, xmax=self.xmax,
                                        bc_left_type=self.bc_left_type,
                                        bc_right_type=self.bc_right_type))

            nx_t *= 2

        # provide coordinate and indexing information for the solution mesh
        self.soln_grid = self.grids[self.nlevels-1]

        self.ilo = self.soln_grid.ilo
        self.ihi = self.soln_grid.ihi

        self.x = self.soln_grid.x
        self.dx = self.soln_grid.dx

        # store the source norm
        self.source_norm = 0.0

        # after solving, keep track of the number of cycles taken and
        # the residual error (normalized to the source norm)

        self.num_cycles = 0
        self.residual_error = 1.e33

    def get_solution(self):
        return self.grids[self.nlevels-1].v.copy()

    def get_solution_object(self):
        return self.grids[self.nlevels-1]

    def init_solution(self):
        """
        initialize the solution to the elliptic problem as zero
        """
        self.soln_grid.v[:] = 0.0

    def init_rhs(self, data):
        self.soln_grid.f[:] = data.copy()

        # store the source norm
        self.source_norm = self.soln_grid.norm(self.soln_grid.f)

    def smooth(self, level, nsmooth):
        """ use Gauss-Seidel iterations to smooth """

        myg = self.grids[level]

        myg.fill_bcs()

        # do red-black G-S
        for _ in range(nsmooth):

            myg.v[myg.ilo:myg.ihi+1:2] = 0.5 * (
                -myg.dx * myg.dx * myg.f[myg.ilo:myg.ihi+1:2] +
                myg.v[myg.ilo+1:myg.ihi+2:2] + myg.v[myg.ilo-1:myg.ihi:2])

            myg.fill_bcs()

            myg.v[myg.ilo+1:myg.ihi+1:2] = 0.5 * (
                -myg.dx * myg.dx * myg.f[myg.ilo+1:myg.ihi+1:2] +
                myg.v[myg.ilo+2:myg.ihi+2:2] + myg.v[myg.ilo:myg.ihi:2])

            myg.fill_bcs()

    def solve(self, rtol=1.e-11):
        """do V-cycles util the L2 norm of the relative solution difference is
        < rtol

        """

        if self.verbose:
            print("source norm = ", self.source_norm)

        residual_error = 1.e33
        cycle = 1

        # diagnostics that are returned -- residual error norm and true
        # error norm (if possible) for each cycle
        rlist = []
        elist = []

        while residual_error > rtol and cycle <= self.max_cycles:

            # zero out the solution on all but the finest grid
            for level in range(self.nlevels-1):
                self.grids[level].v[:] = 0.0

            # descending part
            if self.verbose:
                print(f"<<< beginning V-cycle (cycle {cycle}) >>>\n")

            self.v_cycle(self.nlevels-1)

            # compute the residual error, relative to the source norm
            self.soln_grid.compute_residual()
            residual_error = self.soln_grid.norm(self.soln_grid.r)
            if self.source_norm != 0.0:
                residual_error /= self.source_norm

            if residual_error < rtol:
                self.num_cycles = cycle
                self.residual_error = residual_error
                self.soln_grid.fill_bcs()

            if self.verbose:
                print(f"cycle {cycle}: residual err / source norm = {residual_error:11.6g}\n")

            rlist.append(residual_error)

            if self.true_function is not None:
                elist.append(self.soln_grid.norm(self.soln_grid.v - self.true_function(self.soln_grid.x)))

            cycle += 1

        return elist, rlist

    def v_cycle(self, level):

        if level > 0:
            fp = self.grids[level]
            cp = self.grids[level-1]

            if self.verbose:
                fp.compute_residual()
                old_res_norm = fp.norm(fp.r)

            # smooth on the current level
            self.smooth(level, self.nsmooth)

            # compute the residual
            fp.compute_residual()

            if self.verbose:
                print(f"  level = {level}, nx = {fp.nx:4}, residual change: {old_res_norm:11.6g} -> {fp.norm(fp.r):11.6g}")

            # restrict the residual down to the RHS of the coarser level
            cp.f[:] = fp.restrict(fp.r)

            # solve the coarse problem
            self.v_cycle(level-1)

            # prolong the error up from the coarse grid
            fp.v += cp.prolong(cp.v)

            if self.verbose:
                fp.compute_residual()
                old_res_norm = fp.norm(fp.r)

            # smooth
            self.smooth(level, self.nsmooth)

            if self.verbose:
                fp.compute_residual()
                print(f"  level = {level}, nx = {fp.nx:4}, residual change: {old_res_norm:11.6g} -> {fp.norm(fp.r):11.6g}")

        else:
            # solve the discrete coarse problem just via smoothing
            if self.verbose:
                print("  bottom solve")

            bp = self.grids[0]

            self.smooth(0, self.nsmooth_bottom)

            bp.fill_bcs()

Let’s try this out

def true(x):
    # the analytic solution
    return -np.sin(x) + x*np.sin(1.0)

def f(x):
    # the righthand side
    return np.sin(x)

nx = 128

# create the multigrid object
a = multigrid.Multigrid(nx,
                        bc_left_type="dirichlet", bc_right_type="dirichlet",
                        verbose=1, true_function=true)

# initialize the RHS using the function f
a.init_rhs(f(a.x))

# solve to a relative tolerance of 1.e-11
elist, rlist = a.solve(rtol=1.e-11)

source norm =  0.5221813198632965
<<< beginning V-cycle (cycle 1) >>>

  level = 6, nx =  128, residual change:    0.522181 ->    0.700617
  level = 5, nx =   64, residual change:    0.495162 ->    0.649824
  level = 4, nx =   32, residual change:    0.459083 ->    0.549621
  level = 3, nx =   16, residual change:    0.387872 ->    0.351795
  level = 2, nx =    8, residual change:    0.247396 ->   0.0731208
  level = 1, nx =    4, residual change:   0.0502257 -> 4.11445e-05
  bottom solve
  level = 1, nx =    4, residual change: 3.04921e-05 -> 3.62431e-09
  level = 2, nx =    8, residual change:   0.0618107 -> 0.000937419
  level = 3, nx =   16, residual change:     0.37581 ->  0.00791276
  level = 4, nx =   32, residual change:    0.769146 ->   0.0206557
  level = 5, nx =   64, residual change:     1.23875 ->   0.0291926
  level = 6, nx =  128, residual change:      1.8559 ->   0.0338419
cycle 1: residual err / source norm =   0.0648087

<<< beginning V-cycle (cycle 2) >>>

  level = 6, nx =  128, residual change:   0.0338419 ->   0.0317092
  level = 5, nx =   64, residual change:   0.0224078 ->   0.0270913
  level = 4, nx =   32, residual change:   0.0191314 ->   0.0186129
  level = 3, nx =   16, residual change:   0.0131391 ->  0.00837232
  level = 2, nx =    8, residual change:  0.00591933 ->  0.00171262
  level = 1, nx =    4, residual change:  0.00117663 -> 9.64214e-07
  bottom solve
  level = 1, nx =    4, residual change: 7.14503e-07 -> 8.49423e-11
  level = 2, nx =    8, residual change:  0.00144876 -> 2.21026e-05
  level = 3, nx =   16, residual change:  0.00932633 -> 0.000317085
  level = 4, nx =   32, residual change:   0.0209894 ->   0.0011109
  level = 5, nx =   64, residual change:   0.0339925 ->  0.00188769
  level = 6, nx =  128, residual change:   0.0499314 ->  0.00240723
cycle 2: residual err / source norm =  0.00460995

<<< beginning V-cycle (cycle 3) >>>

  level = 6, nx =  128, residual change:  0.00240723 ->   0.0022994
  level = 5, nx =   64, residual change:  0.00162566 ->  0.00208879
  level = 4, nx =   32, residual change:  0.00147695 ->  0.00170259
  level = 3, nx =   16, residual change:  0.00120312 ->  0.00103128
  level = 2, nx =    8, residual change: 0.000724769 -> 0.000211595
  level = 1, nx =    4, residual change: 0.000145338 -> 1.19054e-07
  bottom solve
  level = 1, nx =    4, residual change: 8.82319e-08 -> 1.04871e-11
  level = 2, nx =    8, residual change:  0.00017885 -> 2.71041e-06
  level = 3, nx =   16, residual change:  0.00108812 -> 2.33868e-05
  level = 4, nx =   32, residual change:  0.00218287 -> 8.87994e-05
  level = 5, nx =   64, residual change:  0.00308115 -> 0.000153082
  level = 6, nx =  128, residual change:  0.00390778 -> 0.000198049
cycle 3: residual err / source norm = 0.000379272

<<< beginning V-cycle (cycle 4) >>>

  level = 6, nx =  128, residual change: 0.000198049 -> 0.000191664
  level = 5, nx =   64, residual change: 0.000135525 ->  0.00017191
  level = 4, nx =   32, residual change:  0.00012151 -> 0.000116464
  level = 3, nx =   16, residual change: 8.21779e-05 ->  3.9485e-05
  level = 2, nx =    8, residual change: 2.79117e-05 -> 7.43198e-06
  level = 1, nx =    4, residual change: 5.10658e-06 ->  4.1854e-09
  bottom solve
  level = 1, nx =    4, residual change: 3.10131e-09 -> 3.68729e-13
  level = 2, nx =    8, residual change: 6.28922e-06 -> 9.62323e-08
  level = 3, nx =   16, residual change: 4.31702e-05 -> 1.83078e-06
  level = 4, nx =   32, residual change: 0.000115963 -> 7.33731e-06
  level = 5, nx =   64, residual change: 0.000191138 -> 1.32008e-05
  level = 6, nx =  128, residual change: 0.000260099 -> 1.72097e-05
cycle 4: residual err / source norm = 3.29573e-05

<<< beginning V-cycle (cycle 5) >>>

  level = 6, nx =  128, residual change: 1.72097e-05 -> 1.65319e-05
  level = 5, nx =   64, residual change: 1.16888e-05 -> 1.45261e-05
  level = 4, nx =   32, residual change: 1.02693e-05 -> 1.06983e-05
  level = 3, nx =   16, residual change: 7.56435e-06 -> 6.40215e-06
  level = 2, nx =    8, residual change: 4.50194e-06 -> 1.32103e-06
  level = 1, nx =    4, residual change: 9.07381e-07 ->   7.433e-10
  bottom solve
  level = 1, nx =    4, residual change: 5.50861e-10 -> 6.54748e-14
  level = 2, nx =    8, residual change: 1.11663e-06 -> 1.69267e-08
  level = 3, nx =   16, residual change: 6.78716e-06 -> 1.47246e-07
  level = 4, nx =   32, residual change: 1.31085e-05 ->  6.2776e-07
  level = 5, nx =   64, residual change: 1.73065e-05 -> 1.16723e-06
  level = 6, nx =  128, residual change: 2.07958e-05 -> 1.54144e-06
cycle 5: residual err / source norm = 2.95193e-06

<<< beginning V-cycle (cycle 6) >>>

  level = 6, nx =  128, residual change: 1.54144e-06 -> 1.48598e-06
  level = 5, nx =   64, residual change: 1.05075e-06 -> 1.32109e-06
  level = 4, nx =   32, residual change: 9.34071e-07 -> 8.83384e-07
  level = 3, nx =   16, residual change: 6.23446e-07 -> 2.31782e-07
  level = 2, nx =    8, residual change: 1.63401e-07 -> 3.53382e-08
  level = 1, nx =    4, residual change:  2.4286e-08 -> 1.99112e-11
  bottom solve
  level = 1, nx =    4, residual change: 1.47525e-11 -> 1.75429e-15
  level = 2, nx =    8, residual change: 2.99243e-08 -> 4.60355e-10
  level = 3, nx =   16, residual change: 2.38669e-07 -> 1.29896e-08
  level = 4, nx =   32, residual change: 8.26216e-07 -> 5.65267e-08
  level = 5, nx =   64, residual change:  1.3865e-06 -> 1.05798e-07
  level = 6, nx =  128, residual change: 1.81761e-06 -> 1.40268e-07
cycle 6: residual err / source norm = 2.68619e-07

<<< beginning V-cycle (cycle 7) >>>

  level = 6, nx =  128, residual change: 1.40268e-07 -> 1.34754e-07
  level = 5, nx =   64, residual change: 9.52817e-08 -> 1.16914e-07
  level = 4, nx =   32, residual change: 8.26508e-08 -> 8.00411e-08
  level = 3, nx =   16, residual change: 5.65961e-08 ->  4.7816e-08
  level = 2, nx =    8, residual change: 3.36554e-08 -> 9.97506e-09
  level = 1, nx =    4, residual change: 6.85178e-09 -> 5.61298e-12
  bottom solve
  level = 1, nx =    4, residual change: 4.15975e-12 -> 4.94433e-16
  level = 2, nx =    8, residual change: 8.43232e-09 -> 1.27905e-10
  level = 3, nx =   16, residual change: 5.12193e-08 -> 1.12547e-09
  level = 4, nx =   32, residual change: 9.52837e-08 -> 4.96598e-09
  level = 5, nx =   64, residual change:  1.2275e-07 -> 9.63633e-09
  level = 6, nx =  128, residual change: 1.45577e-07 -> 1.28961e-08
cycle 7: residual err / source norm = 2.46965e-08

<<< beginning V-cycle (cycle 8) >>>

  level = 6, nx =  128, residual change: 1.28961e-08 ->  1.2395e-08
  level = 5, nx =   64, residual change: 8.76447e-09 -> 1.08791e-08
  level = 4, nx =   32, residual change: 7.69259e-09 -> 7.17337e-09
  level = 3, nx =   16, residual change: 5.06449e-09 ->  1.5655e-09
  level = 2, nx =    8, residual change: 1.09623e-09 -> 1.28153e-10
  level = 1, nx =    4, residual change: 8.81273e-11 -> 7.23224e-14
  bottom solve
  level = 1, nx =    4, residual change: 5.35688e-14 -> 6.37363e-18
  level = 2, nx =    8, residual change: 1.08749e-10 -> 1.70162e-12
  level = 3, nx =   16, residual change: 1.40942e-09 ->  9.9182e-11
  level = 4, nx =   32, residual change: 6.53672e-09 -> 4.61658e-10
  level = 5, nx =   64, residual change:  1.1048e-08 -> 8.88393e-10
  level = 6, nx =  128, residual change: 1.42054e-08 -> 1.19231e-09
cycle 8: residual err / source norm = 2.28332e-09

<<< beginning V-cycle (cycle 9) >>>

  level = 6, nx =  128, residual change: 1.19231e-09 -> 1.14391e-09
  level = 5, nx =   64, residual change: 8.08857e-10 -> 9.85038e-10
  level = 4, nx =   32, residual change: 6.96384e-10 -> 6.43751e-10
  level = 3, nx =   16, residual change: 4.55092e-10 -> 3.80371e-10
  level = 2, nx =    8, residual change: 2.67995e-10 -> 8.01385e-11
  level = 1, nx =    4, residual change: 5.50479e-11 -> 4.50973e-14
  bottom solve
  level = 1, nx =    4, residual change: 3.34209e-14 -> 3.97256e-18
  level = 2, nx =    8, residual change: 6.77507e-11 -> 1.02848e-12
  level = 3, nx =   16, residual change: 4.12047e-10 -> 9.35298e-12
  level = 4, nx =   32, residual change: 7.47687e-10 -> 4.11344e-11
  level = 5, nx =   64, residual change: 9.62859e-10 -> 8.19452e-11
  level = 6, nx =  128, residual change: 1.14364e-09 -> 1.10707e-10
cycle 9: residual err / source norm = 2.12009e-10

<<< beginning V-cycle (cycle 10) >>>

  level = 6, nx =  128, residual change: 1.10707e-10 -> 1.06183e-10
  level = 5, nx =   64, residual change: 7.50834e-11 -> 9.22324e-11
  level = 4, nx =   32, residual change: 6.52181e-11 -> 6.00174e-11
  level = 3, nx =   16, residual change: 4.23901e-11 -> 1.28587e-11
  level = 2, nx =    8, residual change: 8.94185e-12 -> 2.23329e-13
  level = 1, nx =    4, residual change: 1.52558e-13 -> 1.23793e-16
  bottom solve
  level = 1, nx =    4, residual change: 9.19761e-17 -> 1.08809e-20
  level = 2, nx =    8, residual change: 1.85396e-13 -> 2.38713e-15
  level = 3, nx =   16, residual change: 1.01041e-11 -> 7.80254e-13
  level = 4, nx =   32, residual change: 5.45635e-11 -> 3.87589e-12
  level = 5, nx =   64, residual change: 9.16104e-11 -> 7.60695e-12
  level = 6, nx =  128, residual change:  1.1637e-10 ->  1.0298e-11
cycle 10: residual err / source norm =  1.9721e-11

<<< beginning V-cycle (cycle 11) >>>

  level = 6, nx =  128, residual change:  1.0298e-11 -> 9.87413e-12
  level = 5, nx =   64, residual change: 6.97734e-12 -> 8.45531e-12
  level = 4, nx =   32, residual change: 5.97782e-12 -> 5.37496e-12
  level = 3, nx =   16, residual change: 3.79861e-12 -> 3.07967e-12
  level = 2, nx =    8, residual change: 2.17194e-12 -> 6.52951e-13
  level = 1, nx =    4, residual change: 4.48533e-13 -> 3.67473e-16
  bottom solve
  level = 1, nx =    4, residual change: 2.72325e-16 -> 3.23706e-20
  level = 2, nx =    8, residual change: 5.52076e-13 -> 8.38793e-15
  level = 3, nx =   16, residual change: 3.37089e-12 -> 8.09049e-14
  level = 4, nx =   32, residual change: 6.08043e-12 -> 3.48793e-13
  level = 5, nx =   64, residual change: 7.95466e-12 -> 7.06031e-13
  level = 6, nx =  128, residual change: 9.52594e-12 -> 9.61779e-13
cycle 11: residual err / source norm = 1.84185e-12

Notice that it did 11 V-cycles.

We also see that each V-cycle reduces the residual error by about an order of magnitude—this is a good rule-of-thumb for multigrid.

We can also compute the error with respect to the analytic solution (since we know that for this case):

# get the solution 
v = a.get_solution()

# compute the error from the analytic solution
e = v - true(a.x)

print(f"L2 error from true solution = {a.soln_grid.norm(e)}")

L2 error from true solution = 3.8905913165725256e-06

Now let’s plot the solution and how the error changes as a function of cycle

fig = plt.figure()
ax = fig.add_subplot(111)

ax.plot(a.x[a.ilo:a.ihi+1], true(a.x[a.ilo:a.ihi+1]),
        color="0.5", ls=":", label="analytic solution")
ax.scatter(a.x[a.ilo:a.ihi+1], v[a.ilo:a.ihi+1],
           color="C1", label="multigrid solution", marker="+")
ax.set_xlabel("x")
ax.set_ylabel(r"$\phi$")
ax.legend()

<matplotlib.legend.Legend at 0x7f1b1cd38c50>

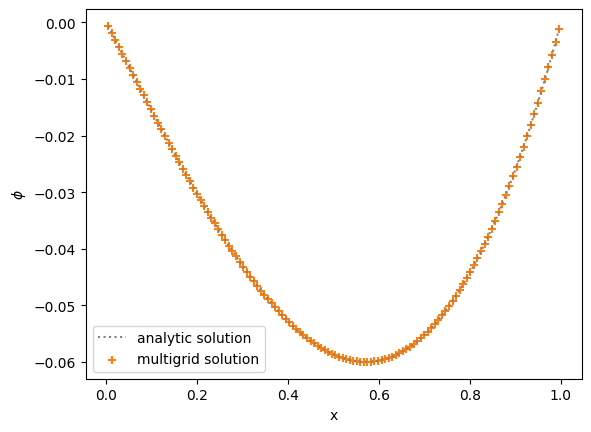
fig = plt.figure()
ax = fig.add_subplot(111)

ncycle = np.arange(len(elist)) + 1

ax.plot(ncycle, elist, label=r"$\| e\|$")
ax.plot(ncycle, rlist, "--", label=r"$\| r\|$")

ax.set_xlabel("# of V-cycles")
ax.set_ylabel("L2 norm of error")

ax.set_yscale('log')

ax.legend()

<matplotlib.legend.Legend at 0x7f1b1c5aa050>

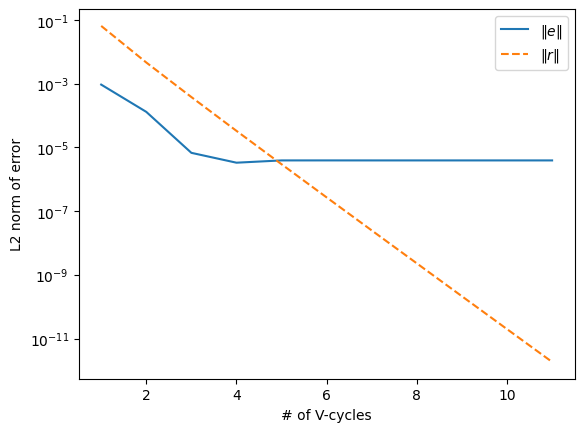
We see the same behavior as we did with smoothing: the true error, \(\| e \|\) stalls because of the truncation error of our discretization, but the residual error, \(\| r \|\) keeps decreasing (at least until it reaches roundoff error).