In-class Example: A Frequency Filter

Let’s see how we can use an FFT to filter high-frequency noise.

We’ll need our DFT functions:

import numpy as np
import matplotlib.pyplot as plt

def dft(f_n):
    """perform a discrete Fourier transform"""
    
    N = len(f_n)
    n = np.arange(N)
    
    f_k = np.zeros((N), dtype=np.complex128)

    for k in range(N):
        f_k[k] = np.sum(f_n * np.exp(-2.0 * np.pi * 1j * n * k / N))
    return f_k

def idft(F_k):
    """perform a discrete Fourier transform"""
    
    N = len(F_k)
    k = np.arange(N)
    
    f_n = np.zeros((N), dtype=np.float64)

    for n in range(N):
        f_n[n] = (1/N) * np.sum(F_k * np.exp(2.0 * np.pi * 1j * n * k / N)).real
    return f_n

Now let’s create a sine wave and add lots of random noise

def f(x, nu=0.2):
    return np.sin(2.0 * np.pi * nu * x) + 0.5 * np.random.randn(len(x))

Let’s look at the function now

xmax = 50
N = 128

x = np.linspace(0.0, xmax, N, endpoint=False)

fig, ax = plt.subplots()
f_n = f(x)
ax.plot(x, f_n)

[<matplotlib.lines.Line2D at 0x7fde20c62b90>]

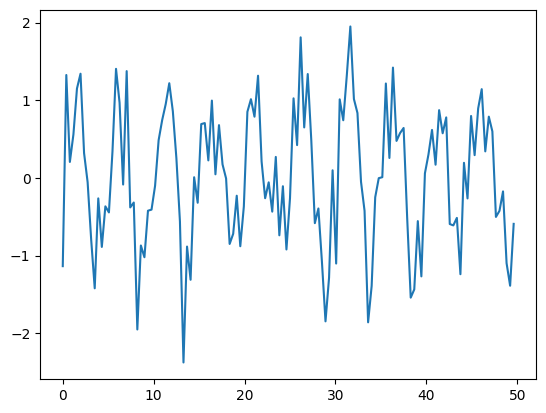
Let’s try to remove this noise by working in frequency space. Here’s our plan:

• Transform our function to frequency space

• Plot the power spectrum to see the structure with frequency

• Zero out the Fourier components of any low-amplitude modes in the power spectrum

• Transform back to real space