Burgers’ Riemann Problem

As discussed with advection, the physics of the equation comes into play when we determine what the correct state is on the interface given a left and right state. This is the Riemann problem. For Burgers’ equation, this Riemann problem is more complex.

Shock speed

If the characteristics intersect in the \(x\)-\(t\) plane, then it is not possible to trace backwards in time to see where the information came from—this is the condition of a shock. The shock speed is computed through the Rankine-Hugoniot jump conditions.

Consider the following space-time diagram:

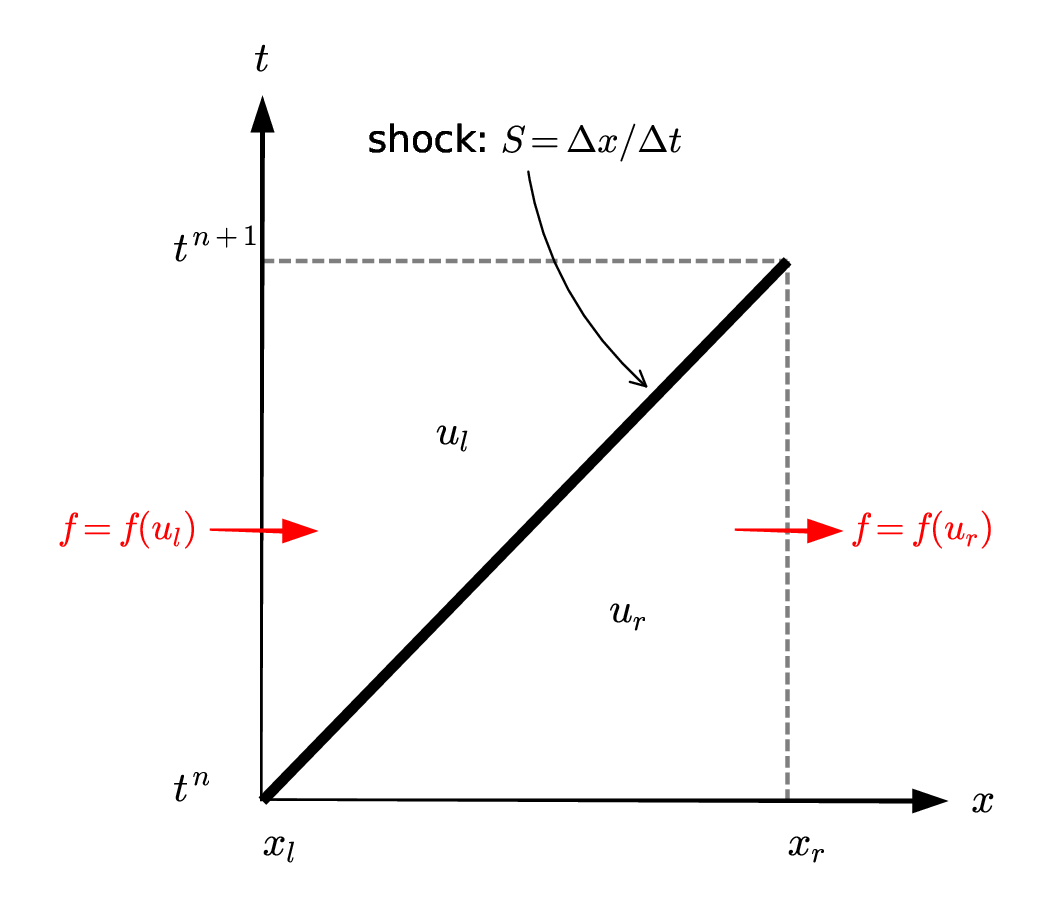
Fig. 8 A rightward moving shock in the \(x\)-\(t\) plane separating two state

This shows a left and right state, \(u_l\) and \(u_r\), separated by a rightward moving shock in the \(x\)-\(t\) plane (the dark line). Notice that:

• At time \(t^n\), the state in our integral \(x \in [x_l, x_r]\) is entirely \(u_r\).

• As time evolves (think about moving upward in this figure), the state becomes a mix of states \(u_l\) and \(u_r\).

• Finally at time \(t^{n+1}\) the state is entirely \(u_l\) in \(x \in [x_l, x_r]\).

• The shock speed is clearly \(S = \Delta x / \Delta t\) in this figure.

To determine the speed, we start with Burgers’ equation in conservative form:

\[u_t = - [f(u)]_x\]

and integrate our conservation law over space and time (and normalize by \(\Delta x\)):

\[\frac{1}{\Delta x} \int_{x_l}^{x_r} dx \int_{t^n}^{t^{n+1}} dt u_t = - \frac{1}{\Delta x} \int_{x_l}^{x_r} dx \int_{t^n}^{t^{n+1}} dt [f(u)]_x\]

Recognizing that at \(t = t^n\), \(u = u_r\) and at \(t = t^{n+1}\), \(u = u_l\), the left side becomes:

\[\frac{1}{\Delta x} \int_{x_l}^{x_r} \left \{ u(t^{n+1}) - u(t^n) \right \} dx = u_l - u_r\]

Now for the right side. We see that all along \(x = x_l\), the flux is \(f = f(u_l)\) for \(t \in [t^n, t^{n+1}]\). Likewise, all along \(x = x_r\), the flux is \(f = f(u_r)\) in the same time interval. Therefore, our expression becomes:

\[(u_l - u_r) = - \frac{\Delta t}{\Delta x} \left [ f(u_r) - f(u_l) \right ]\]

Using \(S = \Delta x/\Delta t\), we see:

\[S = \frac{f(u_r) - f(u_l)}{u_r - u_l}\]

and taking \(f(u) = u^2 / 2\), we get:

\[S = \frac{1}{2} (u_l + u_r)\]

Sampling the solution

Now that we understand the shock speed, we need to determine what the state is on the interface.

For an interface in our domain, \(u_{i+1/2}\), we need to solve the Riemann problem \(u_{i+1/2} = \mathcal{R}(u_{i+1/2,L}, u_{i+1/2,R})\). We do this first by looking at whether the flow is converging or diverging. For converging flow, \(u_{i+1/2,L} > u_{i+1/2,R}\), we need to consider a shock; otherwise we consider a rarefaction. We write this as:

\[\begin{split}u_{i+1/2} = \mathcal{R}(u_{i+1/2,L}, u_{i+1/2,R}) = \left \{ \begin{array}{cc} u_\mathrm{shock} & \mbox{if}~ u_{i+1/2,L} > u_{i+1/2,R} \\ u_\mathrm{rare} & \mbox{otherwise} \end{array} \right . \end{split}\]

where \(u_s\) is the shock case and \(u_r\) is the rarefaction case.

For the shock, we look at the direction the shock is moving and choose the appropriate state:

\[\begin{split}u_\mathrm{shock} = \left \{ \begin{array}{cc} u_{i+1/2,L} & \mbox{if}~ S > 0 \\ u_{i+1/2,R} & \mbox{if}~ S < 0 \end{array} \right . \end{split}\]

For the rarefaction, we do:

\[\begin{split}u_\mathrm{rare} = \left \{ \begin{array}{cc} u_{i+1/2,L} & \mbox{if}~ u_{i+1/2,L} > 0 \\ u_{i+1/2,R} & \mbox{if}~ u_{i+1/2,R} < 0 \\ 0 & \mbox{otherwise} \end{array} \right . \end{split}\]