Floating Point Format

In numerical calculations, we need to worry about several sources of error including floating point and truncation error. Here we will describe these concepts.

Note

Reading: What Every Computer Scientist Should Know About Floating-Point Arithmetic

Storage overview

We can think of a floating point number as having the form:

\[ \mbox{significand} \times 10^\mbox{exponent} \]

Most computers follow the IEEE 754 standard for floating point, and we commonly work with 32-bit and 64-bit floating point numbers (single and double precision). These bits are split between the signifcand and exponent as well as a single bit for the sign:

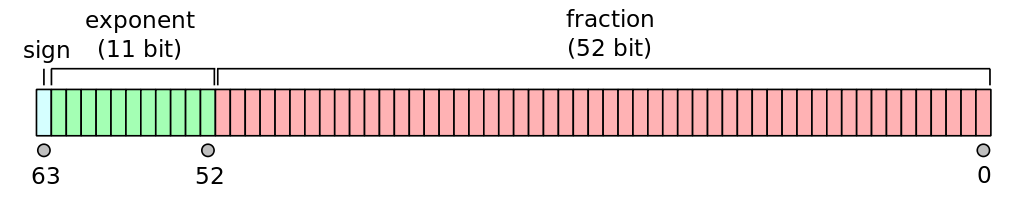
Fig. 2 (source: wikipedia)

Since the number is stored in binary, we can think about expanding a number in powers of 2:

\[ 0.1 \sim (1 + 1 \cdot 2^{-1} + 0 \cdot 2^{-2} + 0 \cdot 2^{-3} + 1 \cdot 2^{-4} + 1 \cdot 2^{-5} + \ldots) \times 2^{-4} \]

In fact, 0.1 cannot be exactly represented in floating point:

python

print(f"{0.1:30.20f}")

C++

#include <iostream>
#include <iomanip>

int main() {

    double a = 0.1;

    std::cout << std::setprecision(19) << a << std::endl;

}

Note

You can interactively explore the floating-point formats at this nice website: float.exposed

Precision

With 52 bits for the significand, the smallest number compared to 1 we can represent is

\[ 2^{-52} \approx 2.22\times 10^{-16} \]

but the IEEE 754 format always expresses the significant such that the first bit is 1 (by adjusting the exponent) and then doesn’t need to store that 1, giving us an extra bit of precision, so the machine epsilon is

\[ 2^{-53} \approx 1.11\times 10^{-16} \]

Note

This is a relative error, so for a number like 1000 we could only add 1.1e-13 to it before it became indistinguishable from 1000.

\[ \mbox{relative roundoff error} = \frac{|\mbox{true number} - \mbox{computer representation} |} {|\mbox{true number}|} \le \epsilon \]

There are varying definitions of machine epsilon which differ by a factor of 2.

Range

Now consider the exponent, we use 11 bits to store it in double precision. Two are reserved for special numbers, so out of the 2048 possible exponent values, one is 0, and 2 are reserved, leaving 2045 to split between positive and negative exponents. These are set as:

\[ 2^{-1022} \mbox{ to } 2^{1023} \]

converting to base 10, this is

\[ \sim 10^{-308} \mbox{ to } \sim 10^{308} \]

Accessing Properties

Most languages have functions that return the basic properties / limits of floating point

python

  import sys
  sys.float_info

C++

#include <iostream>
#include <limits>

int main() {

    std::cout << "maximum double = " << std::numeric_limits<double>::max() << std::endl;
    std::cout << "maximum double base-10 exponent = " << std::numeric_limits<double>::max_exponent10 << std::endl;
    std::cout << "smallest (abs) double = " << std::numeric_limits<double>::min() << std::endl;
    std::cout << "minimum double base-10 exponent = " << std::numeric_limits<double>::min_exponent10 << std::endl;
    std::cout << "machine epsilon (double) = " << std::numeric_limits<double>::epsilon() << std::endl;

}