Example: Matrix

Let’s look at an example from your text that create a very simple matrix container as a vector-of-vectors. The idea is to do something like:

std::vector<std::vector<double>> a;

Visually, this will look like:

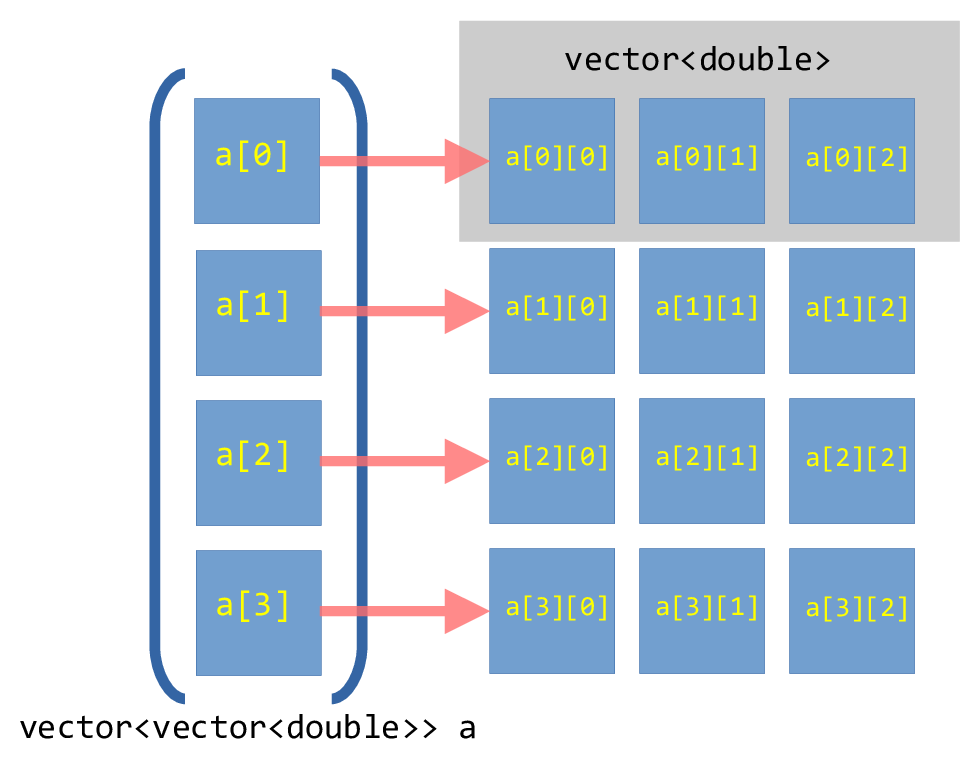
Fig. 5 Illustration of a vector-of-vector’s for a \(4\times 3\) array.

Each row in our matrix is actually a std::vector<double>. To access an individual element, we need to index the first vector to get the row and then index the row to get the column in that row, which will look like: a[irow][jcol].

We’ll write our own version of what the text does.

Listing 11 simple_matrix.cpp

#include <iostream>
#include <vector>

using real_vec_t = std::vector<double>;
using real_mat_t = std::vector<real_vec_t>;

int main() {

    real_mat_t M = {{1.0, 2.0, 3.0, 4.0},
                    {5.0, 6.0, 7.0, 8.0},
                    {9.0, 10.0, 11.0, 12.0}};

    // add another row

    M.push_back({13.0, 14.0, 15.0, 16.0});

    // let's compute the trace (sum over the diagonal)

    double trace{};

    for (std::size_t i = 0; i < M.size(); ++i) {
        trace += M[i][i];
    }

    std::cout << "trace = " << trace << std::endl;

    // now the sum of all the off-diagonal terms

    double off_diag_sum{};

    for (std::size_t irow = 0; irow < M.size(); ++irow) {
        for (std::size_t jcol = 0; jcol < M[irow].size(); ++jcol) {
            if (irow != jcol) {
                off_diag_sum += M[irow][jcol];
            }
        }
    }

    std::cout << "off-diagonal sum = " << off_diag_sum << std::endl;

}

Tip

Notice that we use some type aliases to make it easy to reuse this datatype:

using real_vec_t = std::vector<double>;
using real_mat_t = std::vector<real_vec_t>;

Some comments:

• For our matrix M, M[0] is the first row. It is a vector, and the columns in that row are all stored together in that vector. This is an example of row major ordering of the data.

• To access an element at row irow and column jcol, we do: M[irow][jcol]. The first indexing, M[irow] gives us the vector that holds the row irow data. Then we just index that vector with [jcol] to get the position corresponding to the column we want.

• When we push_back() onto the matrix, we are adding a whole new row.

• When we loop over elements, we first loop over rows (outer loop) and then we loop over the columns in that row—that data is contiguous, so this looping will make the best use of memory cache.

• Both of our operations involve sums over elements—we are careful to first initialize the sum to 0 before adding to it.

Danger

We do nothing here to enforce that every row has the same number of elements—this can potentially be unsafe if we try to access beyond the limits of a row. We’ll fix this later.

Looping over elements

We can loop over elements using range-based loops by first looping over rows and then looping over the columns in the row:

for (auto row : M) {
    for (auto e : row) {
        std::cout << e << " ";
    }
    std::cout << std::endl;
}

Here, the first for loop results in row being a real_vec_t in each iteration, looping over the rows. Then the second for loop gives us a single element in that row (it is a loop over the columns of that row).

This way of looping also demonstrates how the data is stored in the matrix—this is called row-major ordering. We’ll discuss this more shortly.