Example: Multidimensional Contiguous Array

reading

Your text does an example of a multi-dimensional array that is a vector of vector.

We are doing something different here—we want the memory space to be fully contiguous, so we will create a 1-d memory space and create operators to index into it.

`vector`-of-`vector`’s

If we consider:

std::vector<std::vector<double>> array_2d;

Then this is creating a 1-d array that corresponds to the rows of our array, where each element of this is a separate vector to store the columns that make up that row. But each of those row vectors are independent, and can be in very disparate positions in memory.

This is essentially what we did previously as our matrix container.

This can be visualized as:

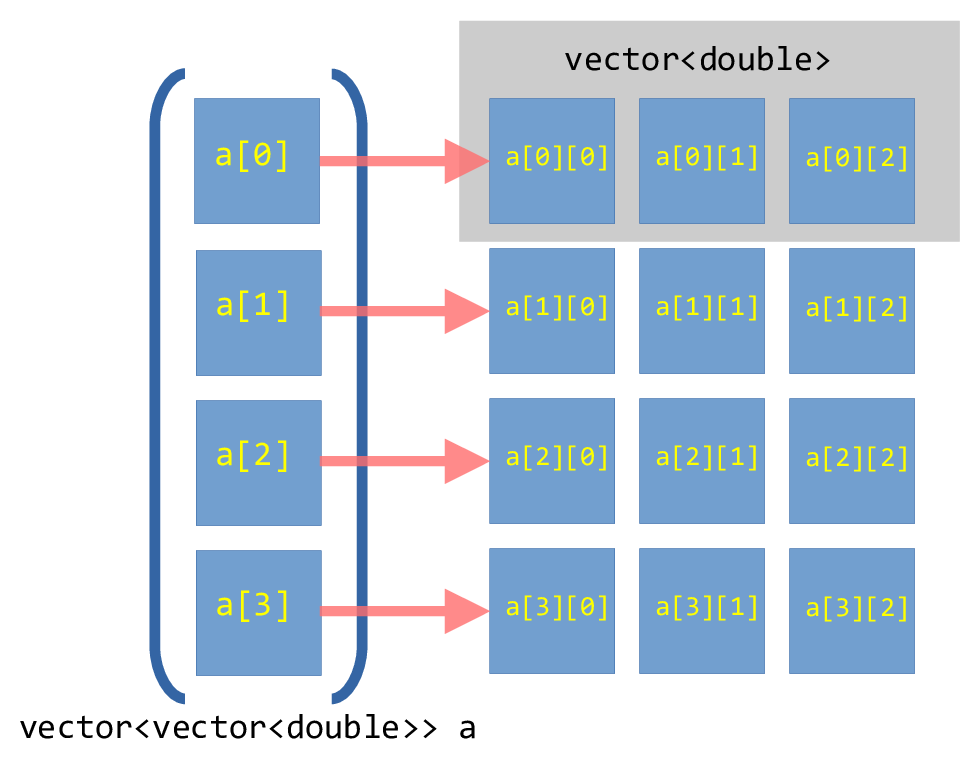
_images/vector_of_vectors.png — Fig. 10 Illustration of a `vector`-of-`vector`’s for a \(4\times 3\) array.

Contiguous multi-dimensional array

Our goal now is to create a contiguous memory space that stores all the elements of the 2-d array.

To make a contiguous vector, we will use a single vector dimensioned with a size of nrows * ncols (note: C++ will likely have more elements than this, to allow for the potential expansion of the vector, but we won’t use that).

We will then overload the () operator to allow for us to index into this one-dimensional buffer as a(nrow, ncol).

This can be visualized as:

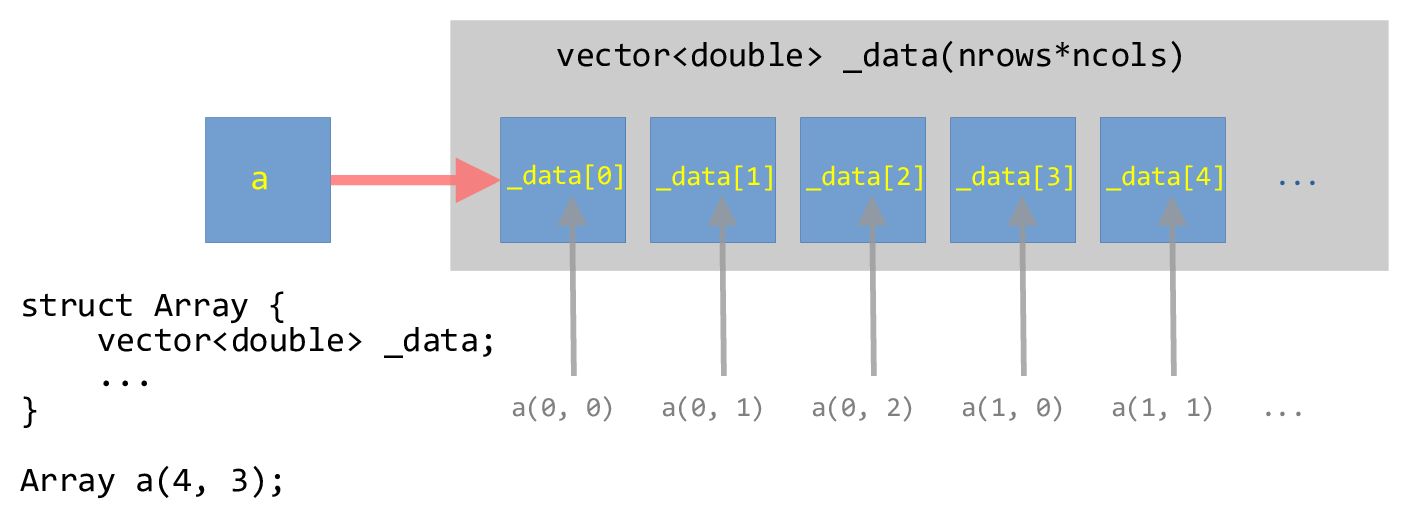
_images/struct_array.png — Fig. 11 Illustration of a one-dimensional `vector` wrapped in a `struct` that can be indexed as a two-dimensional array.

Implementation

We will implement the main struct in a header so we can reuse this

Listing 55 array.H

#ifndef ARRAY_H
#define ARRAY_H

#include <vector>
#include <iostream>
#include <cassert>

// a contiguous 2-d array

// here the data is stored in row-major order in a 1-d memory space
// managed as a vector.  We overload () to allow us to index this as
// a(irow, icol)

struct Array {

    std::size_t _rows;
    std::size_t _cols;
    std::vector<double> _data;

    Array (std::size_t rows, std::size_t cols, double val=0.0)
        : _rows{rows},
          _cols{cols},
          _data(rows * cols, val)
    {
        // we do the asserts here after the initialization of _data
        // in the initialization list, but if the size is zero, we'll
        // abort here anyway.

        assert (rows > 0);
        assert (cols > 0);

    }

    // note the "const" after the argument list here -- this means
    // that this can be called on a const Array

    inline std::size_t ncols() const { return _cols;}
    inline std::size_t nrows() const { return _rows;}

    inline double& operator()(int row, int col) {
        assert (row >= 0 && row < _rows);
        assert (col >= 0 && col < _cols);
        return _data[row*_cols + col];
    }

    inline const double& operator()(int row, int col) const {
        assert (row >= 0 && row < _rows);
        assert (col >= 0 && col < _cols);
        return _data[row*_cols + col];
    }

};

// the << operator is not part of the of the class, so it is not a member

inline
std::ostream& operator<< (std::ostream& os, const Array& a) {

    for (std::size_t row=0; row < a.nrows(); ++row) {
        for (std::size_t col=0; col < a.ncols(); ++col) {
            os << a(row, col) << " ";
        }
        os << std::endl;
    }

    return os;
}

#endif

Some comments on this implementation:

We need to order things in the initialization-list in the same order they appear as member data in the class.
We include the _data vector in the initialization-list without worrying about if its size is zero—the assert in the function body do that for us.
We have two member functions for the () operator. The first is for the case of a non-const declared Array and the second is for a const declared Array.

Here’s a test program for the Array object. Notice that we gain access to the Array class via #include "array.H".

Listing 56 test_array.cpp

#include <iostream>

#include "array.H"

int main() {

    Array x(10, 10);

    for (std::size_t row=0; row < x.nrows(); ++row) {
        for (std::size_t col=0; col < x.ncols(); ++col) {
            if (row == col) {
                x(row, col) = 1.0;
            }
        }
    }

    std::cout << x << std::endl;

    Array y(4, 3);

    double c{0};
    for (auto &e : y._data) {
        e = c;
        c += 1;
    }

    std::cout << y << std::endl;

    // this will fail the assertion
    //std::cout << x(11, 9);

}

Notice a few things:

When we loop over the elements of the Array we get the number of rows via .nrows() and the number of columns via .ncols(). Technically these are of type std::size_t (which is some form of an unsigned int).
For Array y, we use a range-for loop over the elements of _data directly—this is the one-dimensional representation of our array. We can do this because the data is stored contiguously.

Note though—this breaks the idea of encapsulation in a class, since we are accessing this data directly.
When we try to index out of bounds, the assert statements catch this.

Here’s a makefile that builds this test program + a few others that we’ll compare with.

Listing 57 GNUmakefile

ALL: test_array timing fortran_array

# get all the sources and the headers
SOURCE := $(wildcard *.cpp)
HEADERS := $(wildcard *.H)

# create the list of objects by replacing the .cpp with .o for the
# sources
OBJECTS := $(SOURCE:.cpp=.o)

# we have 2 targets here, which means two main() functions.  We need
# to exclude these from the general list of sources / objects, so we
# filter them out
MAINS := test_array.o timing.o test_copy.o
OBJECTS := $(filter-out $(MAINS), $(OBJECTS))

# by default, debug mode will be disabled
DEBUG ?= FALSE

CXXFLAGS := -Wall -Wextra -Wpedantic -Wshadow -g

ifeq (${DEBUG}, TRUE)
   CXXFLAGS += -g
else
   CXXFLAGS += -DNDEBUG -O3
endif

F90FLAGS := -O3 -g

# general rule for compiling a .cpp file to .o
%.o : %.cpp ${HEADERS}
	g++ ${CXXFLAGS} -c $<

%.o : %.f90
	gfortran ${F90FLAGS} -c $<

# the test_array program -- we need to explicitly include
# test_array.o here
test_array: test_array.o ${OBJECTS}
	g++ ${CXXFLAGS} -o $@ test_array.o ${OBJECTS}

# the timing program -- likewise, explicitly include
# timing.o here
timing: timing.o $(OBJECTS)
	g++ ${CXXFLAGS} -o $@ timing.o ${OBJECTS}

fortran_array: fortran_array.o
	gfortran ${F90FLAGS} -o $@ fortran_array.o

# 'make clean' will erase all the intermediate objects
clean:
	rm -f *.o test_array timing fortran_array

Note

The GNUmakefile has some helpful features. To just build as is, we can do:

make

If we instead want to turn on the assert’s, then we do:

make DEBUG=TRUE

To force a rebuild, we can do:

make clean
make

The assert’s are handled by the C++ via the NDEBUG preprocessor directive, so setting -DNDEBUG tells the preprocessor to turn off the asserts.

This GNUmakefile is a little more complex than the previous ones we looked at, since there are several possible targets defined. The first target, test_array in this case, is the default. The other two targets will be discussed below.

try it…

Let’s add .min() and .max() member functions to the class to return the minimum and maximum element in the array respectively.

try it…

What would we need to change if we wanted to make this a class instead of a struct?

Performance

Let’s see how the speed of this compares to doing

std::array<std::array<double, ncols>, nrows>

This needs the size known at compile time, and the array in this case is allocated on the stack instead of the heap. This means that it is likely we will have a stack overflow if we make the array too big.

We’ll also compare to a vector-of-vector, initialized as

std::vector<std::vector<double>> d(nrows, std::vector<double>(ncols, 0.0));

Tip

Here we access a simple clock via <chrono> by calling clock() and use it to time different implementations.

We need to call clock() before and after the code block we are timing to remove any offset in the time returned by clock(). We convert to seconds using CLOCKS_PER_SEC.

Listing 59 timing.cpp

#include <iostream>
#include <cmath>
#include <chrono>
#include <array>

#include "array.H"

constexpr int MAX_SIZE = 10000;

int main() {


    // our Array class

    Array a(MAX_SIZE, MAX_SIZE);

    auto start = clock();

    for (std::size_t irow = 0; irow < a.nrows(); ++irow) {
        for (std::size_t icol = 0; icol < a.ncols(); ++icol) {
            a(irow, icol) = std::sqrt(static_cast<double> (irow + icol + 1));
        }
    }

    auto end = clock();

    std::cout << "Array timing (row-major loop): " <<
        static_cast<double>(end - start) / CLOCKS_PER_SEC << std::endl;

    // again Array, but loop in the wrong order

    Array b(MAX_SIZE, MAX_SIZE);

    start = clock();

    for (std::size_t icol = 0; icol < b.ncols(); ++icol) {
        for (std::size_t irow = 0; irow < b.nrows(); ++irow) {
            b(irow, icol) = std::sqrt(static_cast<double> (irow + icol + 1));
        }
    }

    end = clock();

    std::cout << "Array timing (col-major loop): " <<
        static_cast<double>(end - start) / CLOCKS_PER_SEC << std::endl;

    // fixed-size array
    // Note: this is allocated on the stack and the code crashes
    // on my machine if MAX_SIZE >~ 1000
    // valgrind will also complain

    std::array<std::array<double, MAX_SIZE>, MAX_SIZE> c;

    start = clock();

    for (std::size_t irow = 0; irow < c.size(); ++irow) {
        for (std::size_t icol = 0; icol < c[irow].size(); ++icol) {
            c[irow][icol] = std::sqrt(static_cast<double> (irow + icol + 1));
        }
    }

    end = clock();

    std::cout << "fixed-sized std::array<std::array>>: " <<
        static_cast<double>(end - start) / CLOCKS_PER_SEC << std::endl;


    // vector of vectors

    std::vector<std::vector<double>> d(MAX_SIZE, std::vector<double>(MAX_SIZE, 0.0));

    start = clock();

    for (std::size_t irow = 0; irow < d.size(); ++irow) {
        for (std::size_t icol = 0; icol < d[irow].size(); ++icol) {
            d[irow][icol] = std::sqrt(static_cast<double> (irow + icol + 1));
        }
    }

    end = clock();

    std::cout << "std::vector<std::vector>>: " <<
        static_cast<double>(end - start) / CLOCKS_PER_SEC << std::endl;

}

We can build this via:

make timing

Some things to consider:

Putting the operator() functions in array.H gives the compiler the opportunity to inline them. This can have a big performance difference compared to putting their implementation in a separate C++ file.
We are not timing the array creation. It is likely that creating our Array is more expensive than the std::array<std::array<>> approach.
The std::array<std::array<>> is allocated on the stack, and we can quickly exceed the stack size. Meanwhile, the Array class holds the data on the heap.

try it…

How does the performance change with array size, compiler optimization level, asserts enabled, etc.?

Tip

In our GNUmakefile, we have one additional feature—we are compiling with optimization via -O3. Look to see how the performance changes if we do not optimize.

Finally, we can compare to a Fortran implementation:

Listing 60 fortran_array.f90

program main

  implicit none

  integer, parameter :: MAX_SIZE = 10000

  double precision, allocatable :: a(:,:)
  double precision :: start, end
  integer :: irow, icol

  allocate(a(MAX_SIZE, MAX_SIZE))

  call cpu_time(start)

  do icol = 1, MAX_SIZE
     do irow = 1, MAX_SIZE
        a(irow, icol) = sqrt(dble(irow + icol + 1))
     end do
  end do

  call cpu_time(end)

  print *, "cpu time = ", end - start

end program main

which we can build via

make fortran_array

Example: Multidimensional Contiguous Array

vector-of-vector’s

Contiguous multi-dimensional array

Implementation

Performance

`vector`-of-`vector`’s