Eddington Standard Model

Eddington Standard Model#

Let’s look at the output from the MESA stellar evolution code for 4 different mass progenitors: 0.3, 1, 8, and 15 \(M_\odot\) and see how well the Eddington standard model does in comparison.

Tip

These models were all created using MESA Web a web-based interface to MESA for quick calculations.

To read in these files, we use py_mesa_reader

Tip

py_mesa_reader is available on PyPI, so it can be installed using pip as:

pip install mesa_reader

Loading the data#

import numpy as np
import matplotlib.pyplot as plt
import mesa_reader as mr

MESA provides 2 types of output: profiles and a history. The profiles represent a snapshot of the start at one instance of time and give the stellar data as a function of radius or enclosed mass. The history provides some global quantities as a function of time throughout the entire evolution of the star. We’ll use both.

The model files are:

To make the management easier, we’ll create a container for each model that holds the history and profiles, processed by py_mesa_reader

class Model:
    def __init__(self, mass, profiles=None, history=None):
        self.mass = mass
        if history:
            self.history = mr.MesaData(history)
        self.profiles = []
        if profiles:
            for p in profiles:
                self.profiles.append(mr.MesaData(p))

Now read in all the data. For all but the lowest mass we have 2 profiles and 1 history. The profiles were picked to roughly correspond to the midpoint of core H burning and core He burning.

models = []

models.append(Model(0.3, profiles=["M0.3_default_profile8.data"],
                    history="M0.3_default_trimmed_history.data"))

models.append(Model(1, profiles=["M1_default_profile8.data",
                                 "M1_default_profile218.data"],
                    history="M1_default_trimmed_history.data"))

models.append(Model(8, profiles=["M8_basic_co_profile8.data",
                                 "M8_basic_co_profile39.data"],
                    history="M8_basic_co_trimmed_history.data"))

models.append(Model(15, profiles=["M15_aprox21_profile8.data",
                                  "M15_aprox21_profile19.data"],
                    history="M15_aprox21_trimmed_history.data"))

Creating Eddington profile#

The Eddington standard model works for a fully radiative star with a constant composition.

In class, we found that the temperature and density in the Eddington standard model were related by

\[T(r) = 4.62\times 10^6 \beta\mu \left ( \frac{M}{M_\odot} \right)^{2/3} \rho^{1/3}(r)\]

We will assume that \(\mu\) is constant and take \(\mu\) and \(\beta\) from the center of the star.

# CGS constants
k_B = 1.38e-16
m_u = 1.66e-24
m_e = 9.11e-28
c = 3.e10
h = 6.63e-27
a = 5.67e-15

def get_beta(profile):
    """compute the raito of gas to total pressure"""
    P_g = profile.Rho[0] * k_B * profile.T[0] / (profile.mu[0] * m_u)
    beta = P_g / profile.pressure[0]
    return beta

def eddington_T(rho, beta, mu, M):
    return 4.62e6 * beta * mu * M**(2./3.) * rho**(1./3.)

Here’s our plotting function. We will plot the data from the MESA model and the line corresponding to the Eddington standard model.

def make_plot(profile, beta, M):
    fig, ax = plt.subplots()
    ax.loglog(profile.Rho, profile.T)
    ax.loglog(profile.Rho, eddington_T(profile.Rho, beta, profile.mu[0], M),
              ls=":", label="Eddington standard model")
    ax.legend()
    ax.set_xlabel("rho [g/cc]")
    ax.set_ylabel("T [K]")
    ax.set_title(rf"M = {M} $M_\odot$; age = {profile.star_age/1.e6:.2f} Myr")
    ax.grid(ls=":")

for star in models:
    M = star.mass
    p = star.profiles[0]
    beta = get_beta(p)

    fig = make_plot(p, beta, M)
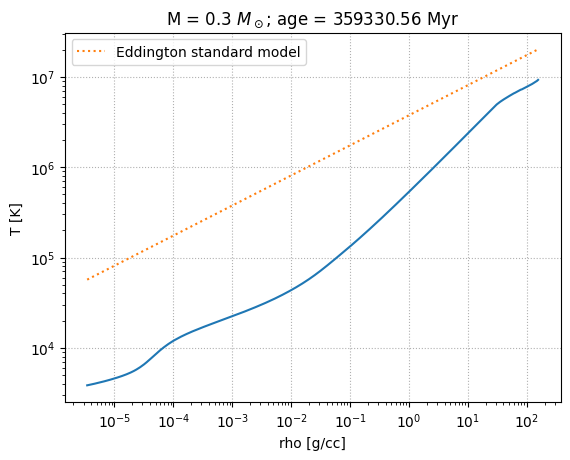
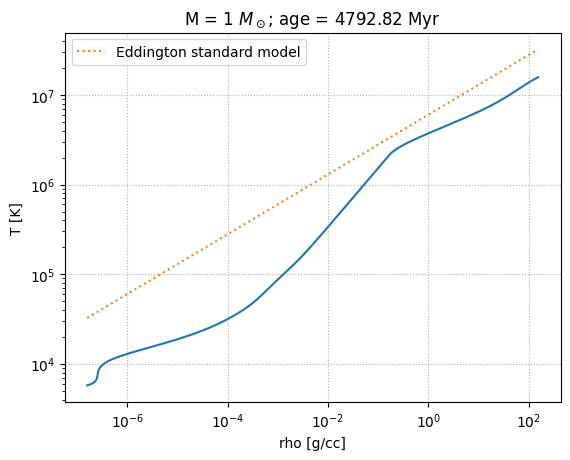
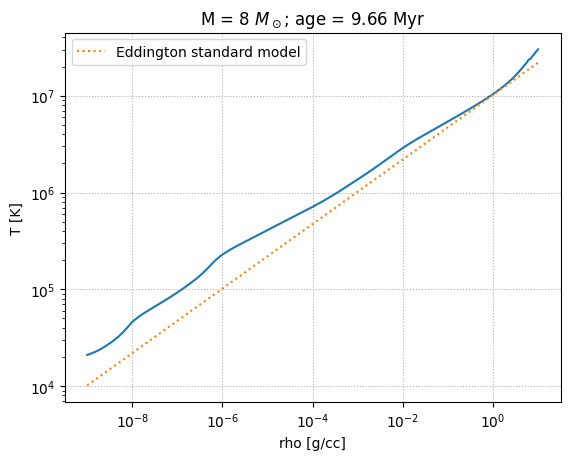
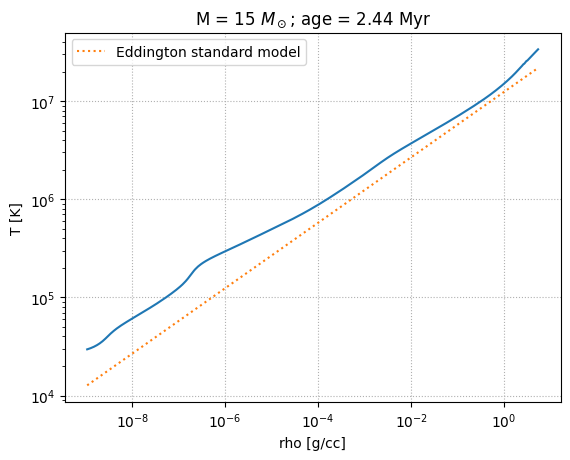
../_images/e58123e43814b9c3814c463a612b49aeb4fe45374ecfc9470f3e27ba9ae5b0f3.png ../_images/9be9ddd876710537686ba854f2d57dfdeb999b22efd2ba4feb4e34f90afd2e23.png ../_images/8a96e25e37434fb70405d0bd07fc7b2c24156be25e4117783dda3f9b0128c1c7.png ../_images/4e09ba4550a60f20b894316186fe40eae7ec9b506b128b3d40fd34bdbc5f435e.png

We see that the high mass stars fit the Eddington profile well.

Contents