Binding Energy per Nucleon

We can explore and plot the binding energy per nucleon to understand when fusion and fission operate.

import pynucastro as pyna

First we’ll get all nuclei with known masses and look at the binding energy

nuclei = pyna.get_all_nuclei()

len(nuclei)

3558

We see there are > 3500 nuclei with measured masses

Most tightly bound nucleus

We can easily find the nucleus that is most tightly bound

nuc_bound = max(nuclei, key=lambda n : n.nucbind)
nuc_bound

Ni62

Binding energy plot

Now we can make a plot of binding energy per nucleon for all nuclei

As = [n.A for n in nuclei]
BEs = [n.nucbind for n in nuclei]

import matplotlib.pyplot as plt

fig, ax = plt.subplots()
ax.scatter(As, BEs, s=5)
ax.set_xlabel("number of nucleons")
ax.set_ylabel("binding energy per nucleon (MeV)")

Text(0, 0.5, 'binding energy per nucleon (MeV)')

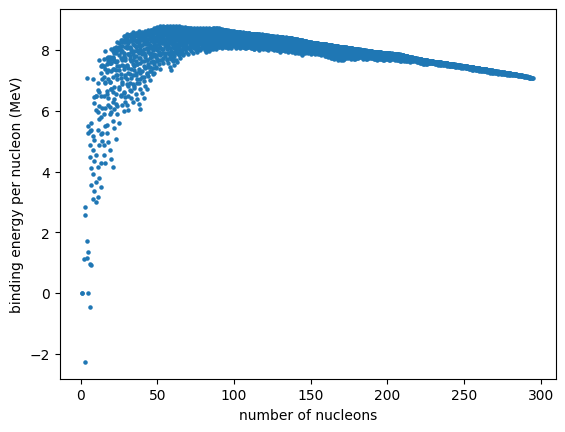
We see that there is quite a spread in binding energy for each nucleon count.

Cleaner plot

We can instead consider only the most tightly bound nucleus at each mass number. We will also only consider those that are stable (or have half lives > 1 million years)

nuc = []

1 million years in seconds

million_years = 1.e6 * 365.25 * 24 * 3600

for A in range(1, max(As)+1):
    # for mass number A, find the nucleus with the maximum binding energy
    try:
        _new = max((n for n in nuclei
                    if n.A == A and (n.tau == "stable" or
                                     (n.tau is not None and n.tau > million_years))),
                   key=lambda q: q.nucbind)
    except ValueError:
        # no stable nucleus of this mass
        continue
    nuc.append(_new)

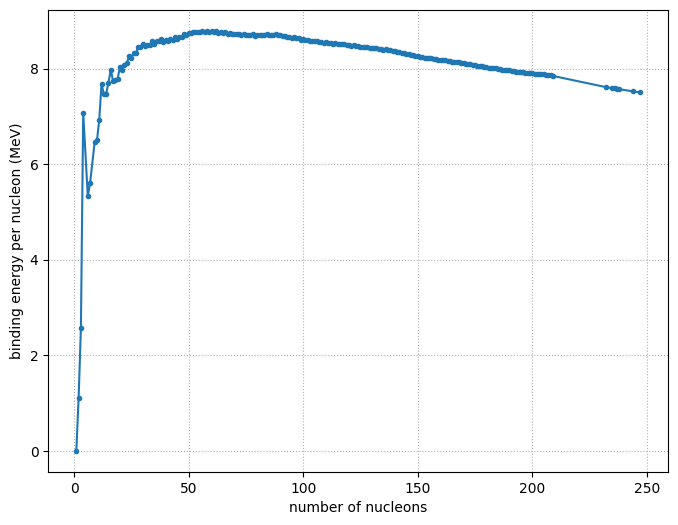
We now plot just these most tightly bound nuclei

As = [n.A for n in nuc]
BEs = [n.nucbind for n in nuc]

fig, ax = plt.subplots()
ax.plot(As, BEs, marker="o", markersize="3")
ax.set_xlabel("number of nucleons")
ax.set_ylabel("binding energy per nucleon (MeV)")
ax.grid(ls=":")
fig.set_size_inches((8, 6))