Floating Point

reading

What Every Computer Scientist Should Know About Floating-Point Arithmetic

Storage overview

We can think of a floating point number as having the form:

\[\mbox{significand} \times 10^\mbox{exponent}\]

Most computers follow the IEEE 754 standard for floating point, and we commonly work with 32-bit and 64-bit floating point numbers (single and double precision). These bits are split between the significand and exponent as well as a single bit for the sign.

Here’s the breakdown for a double type:

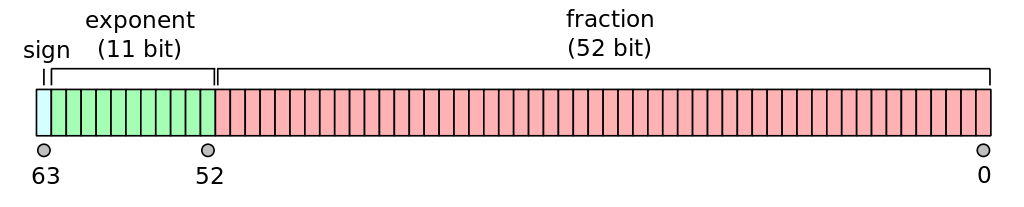
Fig. 5 (source: wikipedia)

Since the number is stored in binary, we can think about expanding a number in powers of 2:

\[0.1 \sim (1 + 1 \cdot 2^{-1} + 0 \cdot 2^{-2} + 0 \cdot 2^{-3} + 1 \cdot 2^{-4} + 1 \cdot 2^{-5} + \ldots) \times 2^{-4}\]

In fact, 0.1 cannot be exactly represented in floating point:

Listing 7 simple_roundoff.cpp

#include <iostream>
#include <iomanip>

int main() {

    double a = 0.1;

    std::cout << std::setprecision(19) << a << std::endl;

}

Note

Here we are using std::setprecision from the iomanip library to force the output to have more decimal places.

Precision

With 52 bits for the significand, the smallest number compared to 1 we can represent is

\[2^{-52} \approx 2.22\times 10^{-16}\]

but the IEEE 754 format always expresses the significant such that the first bit is 1 (by adjusting the exponent) and then doesn’t need to store that 1, giving us an extra bit of precision, so the machine epsilon is

\[2^{-53} \approx 1.11\times 10^{-16}\]

We already saw how to access the limits of the data type via std::numeric_limits. We call this number machine epsilon. It is the smallest number that, when added to 1.0 gives a number distinct from 1.0. We can use the == operator to check this.

Listing 8 epsilon.cpp

#include <iostream>
#include <limits>

int main() {

    double x{1.0};
    double eps{1.11e-16};

    // is x + eps the same as x?

    bool test = x + eps == x;

    std::cout << "x + eps == x: " << test << std::endl;

    // the C++ standard library can also tell us epsilon

    std::cout << "epsilon = " << std::numeric_limits<double>::epsilon() << std::endl;

}

Note that this is a relative error, so for a number like 1000 we could only add 1.1e-13 to it before it became indistinguishable from 1000.

\[\mbox{relative roundoff error} = \frac{|\mbox{true number} - \mbox{computer representation} |} {|\mbox{true number}|} \le \epsilon\]

Note that there are varying definitions of machine epsilon which differ by a factor of 2.

Range

Now consider the exponent, we use 11 bits to store it in double precision. Two are reserved for special numbers, so out of the 2048 possible exponent values, one is 0, and 2 are reserved, leaving 2045 to split between positive and negative exponents. These are set as:

\[2^{-1022} \mbox{ to } 2^{1023}\]

converting to base 10, this is

\[\sim 10^{-308} \mbox{ to } \sim 10^{308}\]

Testing for equality

Because of roundoff error, we should never exactly compare two floating point numbers, but instead ask they they agree within some tolerance, e.g., test equality as:

\[| x - y | < \epsilon\]

For example:

Listing 9 comparing.cpp

#include <iostream>

int main() {

    double h{0.1};
    double sum{0.0};

    // later well learn how to do a loop, but for now
    // we'll explicitly add 10 h's

    sum += h;
    sum += h;
    sum += h;
    sum += h;
    sum += h;
    sum += h;
    sum += h;
    sum += h;
    sum += h;
    sum += h;

    std::cout << "sum == 1:        "
              << (sum == 1.0) << std::endl;

    std::cout << "|sum - 1| < tol: "
              << (std::abs(sum - 1.0) < 1.e-10)
              << std::endl;

}