Roundoff vs. truncation error

Consider the Taylor expansion of \(f(x)\) about some point \(x_0\):

\[f(x) = f(x_0 + \Delta x) = f(x_0) + \left . \frac{df}{dx} \right |_{x_0} \Delta x + \mathcal{O}(\Delta x^2)\]

where \(\Delta x = x - x_0\)

We can solve for the derivative to find an approximation for the first derivative:

\[\left . \frac{df}{dx} \right |_{x_0} = \frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x} + \mathcal{O}(\Delta x)\]

This shows that this approximation for the derivative is first-order accurate in \(\Delta x\)—that is the truncation error of the approximation.

We can see the relative size of roundoff and truncation error by using this approximation to compute a derivative for different values of \(\Delta x\):

Listing 50 truncation_vs_roundoff.cpp

#include <iostream>
#include <iomanip>
#include <cmath>
#include <limits>
#include <vector>

double f(double x) {
    return std::sin(x);
}

double dfdx_true(double x) {
    return std::cos(x);
}

struct point {
    double dx;
    double err;
};

int main() {

    double dx = 0.1;
    double x0 = 1.0;

    std::vector<point> data;

    while (dx > std::numeric_limits<double>::epsilon()) {

        point p;
        p.dx = dx;

        double dfdx_approx = (f(x0 + dx) - f(x0)) / dx;
        double err = std::abs(dfdx_approx - dfdx_true(x0));

        p.err = err;

        data.push_back(p);

        dx /= 2.0;
    }

    std::cout << std::setprecision(8) << std::scientific;

    for (auto p : data) {
        std::cout << std::setw(10) << p.dx << std::setw(15) << p.err << std::endl;
    }
}

It is easier to see the behavior if we make a plot of the output:

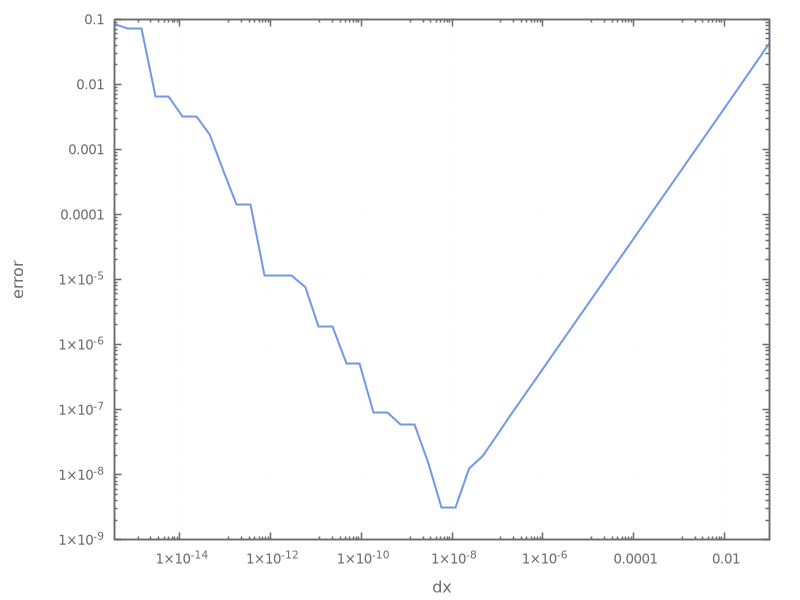
Let’s discuss the trends:

• Starting with the largest value of \(\Delta x\), as we make \(\Delta x\) smaller, we see that the error decreases. This is following the expected behavior of the truncation error derived above.

• Once our \(\Delta x\) becomes really small, roundoff error starts to dominate. In effect, we are seeing that:

  \[(x_0 + \Delta x) - x_0 \ne 0\]

  because of roundoff error.

• The minimum error here is around \(\sqrt{\epsilon}\), where \(\epsilon\) is machine epsilon.