hot-CNO and breakout

hot-CNO and breakout#

import pynucastro as pyna

This collection of rates has the main CNO rates plus a breakout rate into the hot CNO cycle(s)

rl = pyna.ReacLibLibrary()

We’ll get all the rates linking the core nuclei in CNO and the various hot-CNO cycles, but we’ll explicitly remove \(3\)-\(\alpha\), since it is not strong at the temperatures where CNO operates.

linking_nuclei = ["p", "he4",
                  "c12", "c13",
                  "n13", "n14", "n15",
                  "o14", "o15",]
lib = rl.linking_nuclei(linking_nuclei, with_reverse=False)
r3a = lib.get_rate_by_name("he4(aa,g)c12")
lib.remove_rate(r3a)

rc = pyna.RateCollection(libraries=lib)

To evaluate the rates, we need a composition. This is defined using a list of Nucleus objects.

comp = pyna.Composition(rc.get_nuclei())
comp.set_solar_like()

Transition from CNO to hot-CNO#

Let’s look at the CNO cycle at a temperature and density just a bit hotter than the Sun’s core

T = 2.e7
rho = 200

fig = rc.plot(rho=rho, T=T, comp=comp, ydot_cutoff_value=1.e-20)
../_images/44c40159d77b45e1286d4f8b3f9d8d7987a08a0e43a7fe4b6588a13729d07a2e.png

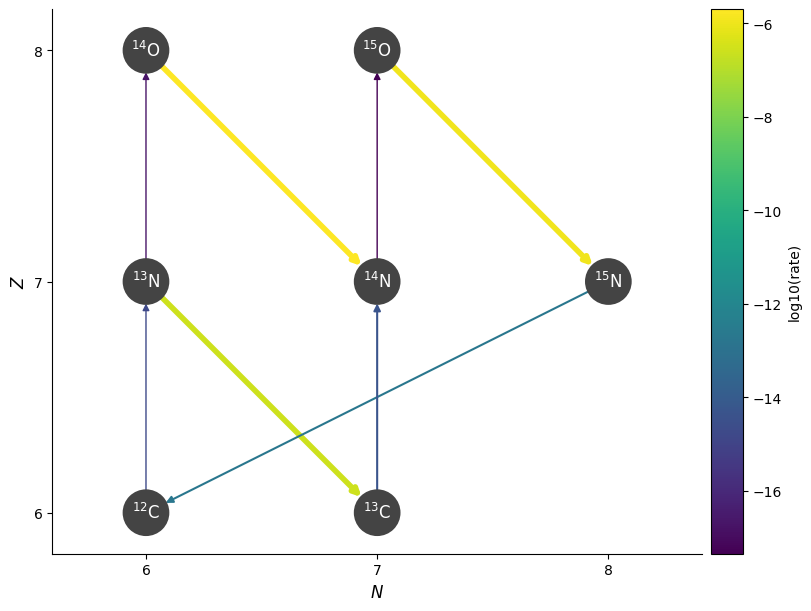
Starting at \({}^{12}\mathrm{C}\), we see the following sequence dominate:

  • We capture a proton to make \({}^{13}\mathrm{N}\)

  • \({}^{13}\mathrm{N}\) almost immediately beta decays to \({}^{13}\mathrm{C}\), since the beta-decay rate is so much faster than a proton capture on \({}^{13}\mathrm{N}\).

  • We continue with proton captures, making \({}^{14}\mathrm{N}\) and then \({}^{15}\mathrm{O}\)

  • \({}^{15}\mathrm{O}\) then beta-decays to get \({}^{15}\mathrm{N}\)

  • Finally, one last proton capture, doing \({}^{15}\mathrm{N}(p,\alpha){}^{12}\mathrm{C}\), getting us back to where we started.

This is the basic CNO cycle

Now let’s make it a bit hotter

T = 3.e8
fig = rc.plot(rho=rho, T=T, comp=comp, ydot_cutoff_value=1.e-20)
../_images/295af0af0a349a91009d6b4af73652bf98492a8267ea625ed994342a255712ec.png

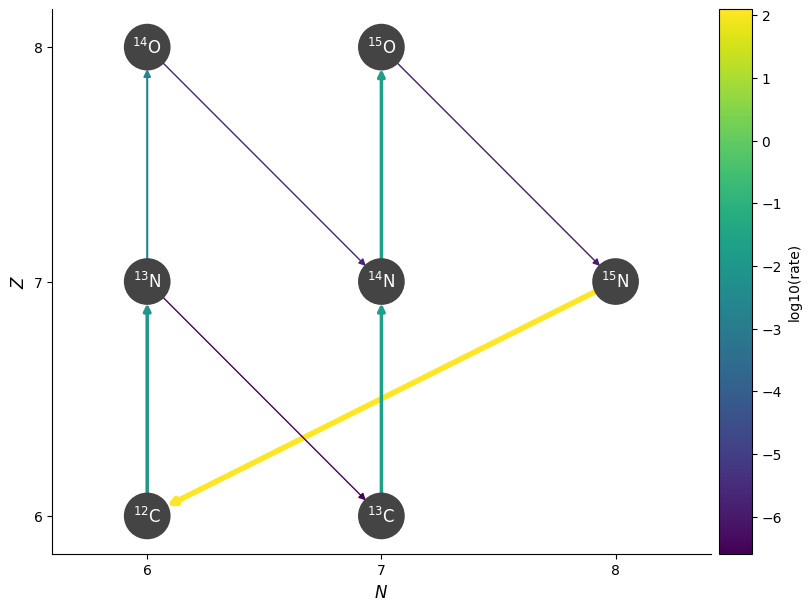
Now we see that the proton capture on \({}^{13}\mathrm{N}\) is faster than the beta-decay, and we make \({}^{14}\mathrm{O}\). Then the cycle continues as before.

As we increase the temperature and density further, we see that the beta decays become the rate-limiting steps.

T = 5.e8
rho = 1.e4
fig = rc.plot(rho=rho, T=T, comp=comp, ydot_cutoff_value=1.e-20)
../_images/f7737dd44a9bd164a734a240567e00ed8dc92112b46ce550419a6475c4946e86.png

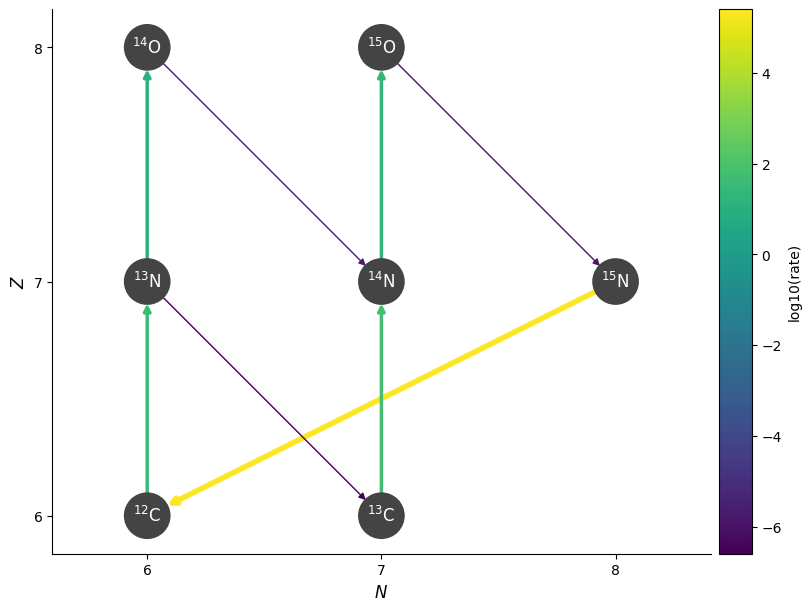
Since the beta-decays are temperature independent (you just have to wait for the nucleus to decay), the overall hot-CNO rate becomes insensitive to temperature.

When does hot-CNO set in?#

We can look at the temperature where we cross from CNO to hot-CNO by looking at the rates involving \({}^{13}\mathrm{N}\)

r1 = rl.get_rate_by_name("n13(p,g)o14")
r2 = rl.get_rate_by_name("n13(,)c13")

import numpy as np
import matplotlib.pyplot as plt

T = np.logspace(7.5, 8.5, 100)

rate_p_capture = [r1.eval(temp) for temp in T]
rate_beta_decay = [r2.eval(temp) for temp in T]

fig, ax = plt.subplots()
ax.plot(T, rate_p_capture, label=r"${}^{13}\mathrm{N}(p,\gamma){}^{14}\mathrm{O}$")
ax.plot(T, rate_beta_decay, label=r"${}^{13}\mathrm{N} \rightarrow {}^{13}\mathrm{C}$")
ax.legend()
ax.set_xscale("log")
ax.set_yscale("log")
../_images/3bee4dab06adcdc90e8c186cd69b52e411c1fb15a893fe19e5f38825f15d4d80.png

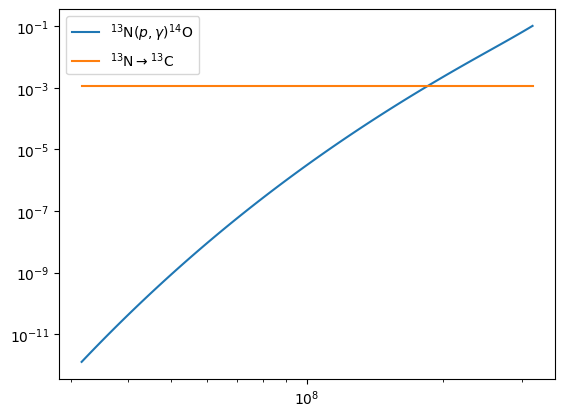
We see that above \(T \sim 2\times 10^8~\mathrm{K}\), the proton-capture proceeds faster than the beta-decay, and we transition to hot-CNO.

Contents