First-Order Accurate Time Update

Let’s start with a first-order update in time. We can use the basic Euler method:

\[\frac{\partial \langle a \rangle}{\partial t} \approx \frac{\langle a\rangle^{n+1} - \langle a\rangle^{n}}{\Delta t}\]

in which case our update appears as:

\[\langle a\rangle_i^{n+1} = \langle a\rangle_i^{n} - \frac{\Delta t}{\Delta x} (F_{i+1/2}^n - F_{i-1/2}^n)\]

We expect this to be first order accurate in time. Notice that the fluxes are evaluated at the old time—this method is explicit.

Reconstruction and the Riemann problem

We need the value of the flux on the interface, \(F_{i+1/2}\), we find this using the analytic expression for the flux, \(F(a)\), as:

\[[F(a)]_{i+1/2} = F(a_{i+1/2})\]

So now we need to find the interface state, \(a_{i+1/2}\).

Note

Getting the value of \(a\) on the interface from the average, \(\langle a \rangle\) is called reconstruction. It means we need to infer how \(a\) actually varies throughout the cell just from the information we have about its average value.

There are a variety of methods we can use (some of which we will explore later). For now, we will do the simplest, and assume that \(a(x)\) is constant in each cell:

\[a_{i+1/2,L} = \langle a\rangle_i^n\]

\[a_{i+1/2,R} = \langle a\rangle_{i+1}^n\]

Notice that we actually have 2 values for the interface state when we do this, one coming from each side of the interface—we label these as the left and right states:

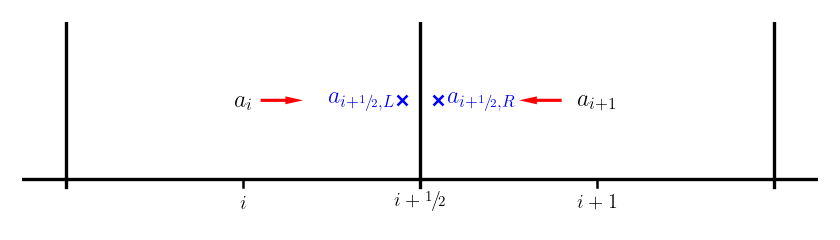
Now we need to resolve this degeneracy—which of the two states (or what combination of them) is the correct interface state? This is called the Riemann problem.

Note

The Riemann problem is where the physics of the actual set of equations comes into play. Thus far, everything we’ve done has been general.

For advection, the Riemann problem is easy. We know that for \(u > 0\) that \(a(x)\) moves from left to right, so the correct state on the interface is the left state—this is upwinding.

\[\begin{split} a_{i+1/2} = \mathcal{R}(a_{i+1/2,L}, a_{i+1/2,R}) = \left \{ \begin{array}{c} a_{i+1/2,L} \quad u > 0 \\ a_{i+1/2,R} \quad u < 0 \end{array} \right . \end{split}\]

where we indicate the Riemann problem as \(\mathcal{R}(a_{i+1/2,L},a_{i+1/2,R})\).

For the advection equation, with \(u > 0\), our interface states are

\[F_{i+1/2} = F(a_{i+1/2}) = u a_{i+1/2} = u \langle a \rangle_i\]

\[F_{i-1/2} = F(a_{i-1/2}) = u a_{i-1/2} = u \langle a \rangle_{i-1}\]

Inserting these into our difference equation, we have:

\[\langle a \rangle_i^{n+1} = \langle a \rangle_i^n - \frac{u \Delta t}{\Delta x} (\langle a \rangle_i^n - \langle a \rangle_{i-1}^n)\]