A Grid Class and Ghost Cells

Consider constructing a derivate using a difference approximation of the form:

\[\frac{\partial a}{\partial x} \approx \frac{a_{i+1} - a_{i-1}}{2 \Delta x}\]

Now imagine that our grid has \(N\) zones, indexed by \(i = 0, 1, \ldots, N-1\). Our difference approximation for \(\partial a/\partial x |_{i=0}\) is:

\[\left .\frac{\partial a}{\partial x} \right |_{i=0} \approx \frac{a_1 - a_{-1}}{2\Delta x}\]

But we don’t have a value of \(a\) corresponding to \(i=-1\).

This is where our boundary conditions come into play, and to accomodate our boundary conditions and allow ourselves to use the same difference approximation everywhere in the domain, we extend the grid using ghost cells.

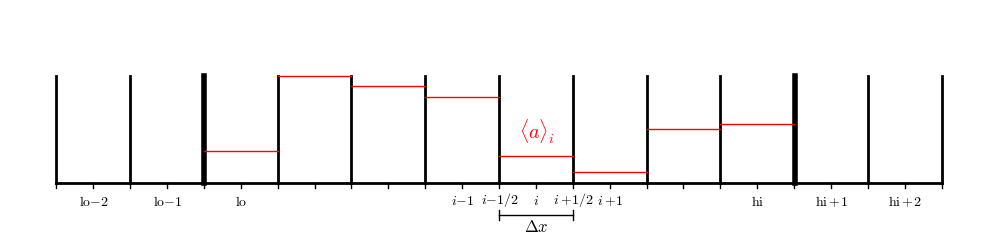
In the figure above, the first zone inside the domain is indexed using lo and the last zone in the domain is indexed with hi. Outside of the domain, there are 2 ghost cells on each end—we will initialize the data in these cells using our knowledge of the boundary conditions.

We need a class that holds the data on a finite-volume grid, including ghost cells. Here’s our implementation:

import numpy as np
import matplotlib.pyplot as plt

class FVGrid:

    def __init__(self, nx, ng=2, xmin=0.0, xmax=1.0):

        self.xmin = xmin
        self.xmax = xmax
        self.ng = ng
        self.nx = nx

        # python is zero-based.  Make easy integers to know where the
        # real data lives
        self.ilo = ng
        self.ihi = ng+nx-1

        # physical coords -- cell-centered, left and right edges
        self.dx = (xmax - xmin)/(nx)
        self.x = xmin + (np.arange(nx+2*ng)-ng+0.5)*self.dx
        self.xl = xmin + (np.arange(nx+2*ng)-ng)*self.dx
        self.xr = xmin + (np.arange(nx+2*ng)-ng+1.0)*self.dx

        # storage for the solution
        self.a = self.scratch_array()
        self.ainit = self.scratch_array()

    def __str__(self):
        return f"nx={self.nx}, ng={self.ng}, xmin={self.xmin}, xmax={self.xmax}"
    
    def __repr__(self):
        return f"FVGrid({self.nx}, ng={self.ng}, xmin={self.xmin}, xmax={self.xmax})"

    def scratch_array(self):
        """ return a scratch array dimensioned for our grid """
        return np.zeros((self.nx+2*self.ng), dtype=np.float64)

    def fill_BCs(self, atmp):
        """ fill all ghostcells with periodic boundary conditions """

        # left boundary
        for n in range(self.ng):
            atmp[self.ilo-1-n] = atmp[self.ihi-n]

        # right boundary
        for n in range(self.ng):
            atmp[self.ihi+1+n] = atmp[self.ilo+n]

    def norm(self, e):
        """ return the norm of quantity e which lives on the grid """
        if not len(e) == (2*self.ng + self.nx):
            return None

        return np.sqrt(self.dx*np.sum(e[self.ilo:self.ihi+1]**2))
    
    def plot(self):
        fig = plt.figure()
        ax = fig.add_subplot(111)

        ax.plot(self.x, self.ainit, label="initial conditions")
        ax.plot(self.x, self.a)
        ax.legend()
        return fig

Let’s test this out to see how the ghost cell filling works. The above implementation does periodic boundaries.

g = FVGrid(10)
g

FVGrid(10, ng=2, xmin=0.0, xmax=1.0)

We can access the data on the grid as g.a[], and the valid data lives in g.a[g.ilo:g.ihi+1] (remembering that range is up to, but not including ihi+1)

g.a[g.ilo:g.ihi+1] = np.arange(g.nx)+1
g.a

array([ 0.,  0.,  1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9., 10.,  0.,
        0.])

Now we can fill ghost cells. For later flexibility, the fill_BCs() method takes an argument which is the array we are filling ghost cells on

g.fill_BCs(g.a)
g.a

array([ 9., 10.,  1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9., 10.,  1.,
        2.])

There are some other useful methods in this class that we will explore later.

Interface values

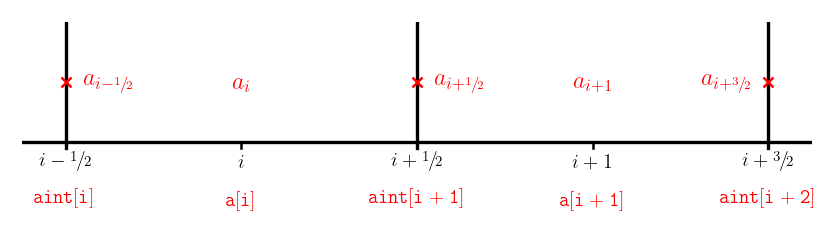
Sometimes need to store interface values (which we’ve been denoting with half-integer subscripts, like \(a_{i-1/2}\)) as arrays which only take integer indices. We will adopt the common convention that when an array refers to an interface state, it denotes the left interface of a cell.

E.g., aint[i]} means \(a_{i-1/2}\)

This is illustrated below for arrays a[] which stores cell center quantities and aint[] which stores interface values: