Two-dimensional Advection

The linear advection equation in 2-d is:

\[a_t + u a_x + v a_y = 0\]

In conservative form, we’d write this as:

\[\frac{\partial a}{\partial t} + \frac{\partial (u a)}{\partial x} + \frac{\partial (v a)}{\partial y} = 0\]

We can develop a finite volume method by defining an average as:

\[\langle a \rangle_{i,j} = \frac{1}{\Delta x \Delta y} \int_{x_{i-1/2}}^{x_{i+1/2}} \int_{y_{j-1/2}}^{y_{j+1/2}} a(x, y) dx dy\]

and our final update would look like (dropping the \(\langle \rangle\)):

\[\frac{\partial}{\partial t} a_{i,j} = - \frac{1}{\Delta x} (F^{(x)}_{i+1/2,j} - F^{(x)}_{i-1/2,j}) - \frac{1}{\Delta y} (F^{(y)}_{i,j+1/2} - F^{(y)}_{i,j-1/2})\]

where \(F^{(x)} = u a\) and \(F^{(y)} = v a\).

This can be solved using the same method-of-lines technique we did in 1-d, but now we need to create and manage a 2-d grid, fill ghost cells on both \(x\) and \(y\) boundaries, and compute fluxes through both \(x\) and \(y\) interfaces.

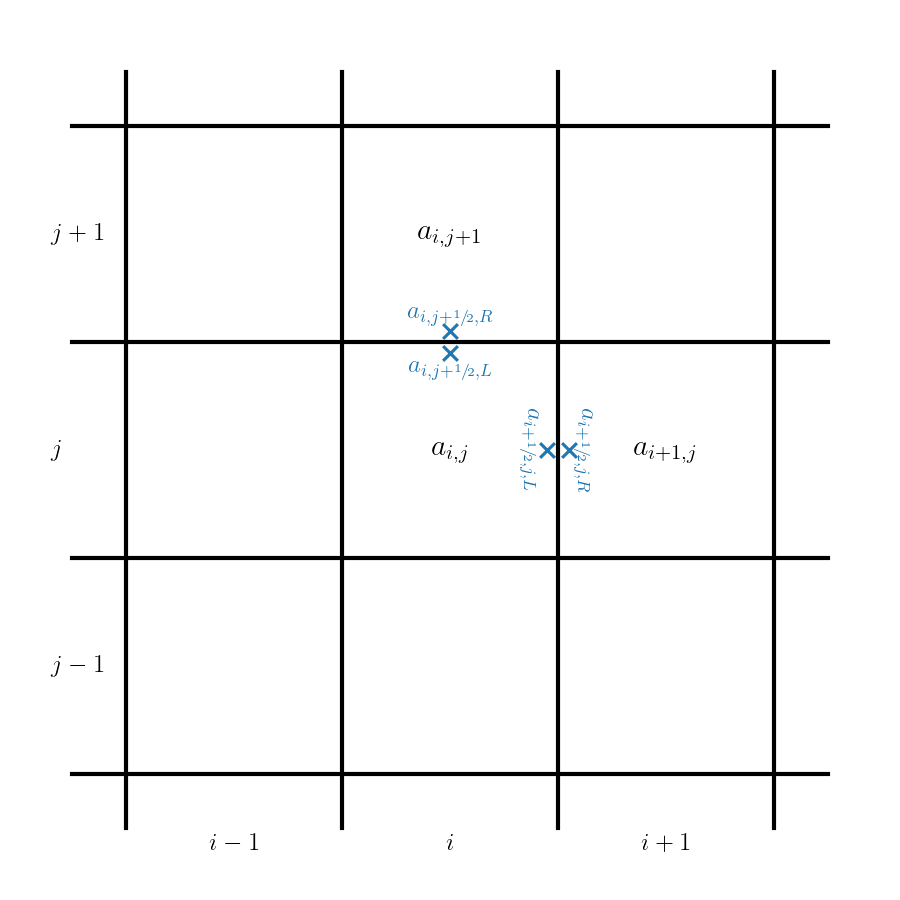
The flux computations are done simply by reconstructing in one coordinate direction and solving the Riemann problem in that direction.

The timestep limiter needs to be adapted a bit, and is now:

\[\Delta t = C \left [ \frac{u}{\Delta x} + \frac{v}{\Delta y} \right ]^{-1}\]

Try it

Code up a 2-d advection solver and test it on advecting a Gaussian.