Piecewise Parabolic Reconstruction for Advection#
In class, we considered piecewise constant and piecewise linear reconstruction with advection. The next step is piecewise parabolic reconstruction. This is described originally here:
The Piecewise Parabolic Method (PPM) for Gas-Dynamical Systems
We want to try this with our method-of-lines integration scheme, which considerably simplifies things compared to that original paper.
Here’s an example of piecewise parabolic reconstruction of data in each zone:
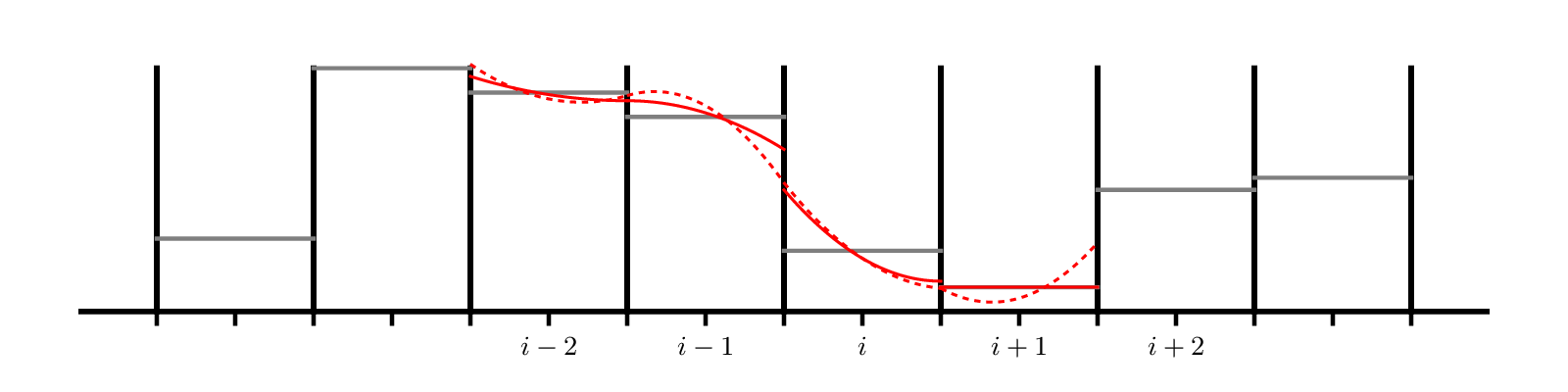
As with piecewise linear, we will need to limit the parabola to prevent overshoots. The dotted lines in the figure above are unlimited parabolas and the solid lines are the limited parabola.
The basic idea is as follows:
In each zone, we construct a parabola, given by CW Eq. 1.4. The CW paper uses \(\xi\) as the space coordinate, were \(\xi_i\) is a zone center and \(\xi_{i-1/2}\) and \(\xi_{i+1/2}\) are the left and right edges. It also allows for a non-uniformly spaced grid.
The parabola has the form:
\[a(\xi) = a_{L,i} + x [ \Delta a_i + a_{6,i} (1 - x) ]\]where
\[x = \frac{\xi - \xi_{i-1/2}}{\Delta \xi}\]and
\[\Delta a_i = a_{R,i} - a_{L,i}\]\[a_{6,i} = 6 \left [ a_i - \frac{1}{2} (a_{L,i} + a_{R,i}) \right ]\]Eqs. 1.5 through 1.10 give the method for computing the 3 coefficients of the parabola for each cell as well as limiting them so as to not introduce any new extrema.
For a uniform grid, the steps are:
Find the first guess at the interface values:
\[a_{i+1/2} = \frac{1}{2} (a_i + a_{i+1}) + \frac{1}{6} (\delta a_i - \delta a_{i+1} )\]with
\[\begin{split}\delta a_i = \left \{ \begin{array}{cc} \min\left (\frac{1}{2}|a_{i+1} - a_{i-1}|, 2 |a_{i+1} - a_i|, 2 |a_i - a_{i-1}|\right ) \mathrm{sign}(a_{i+1} - a_{i-1}) & \mbox{if}\ (a_{i+1} - a_i)(a_i - a_{i-1}) > 0 \\ 0 & \mbox{otherwise} \end{array} \right .\end{split}\]Next, for zone \(i\), set the left and right interface values using the above:
\[a_{L,i} = a_{i-1/2}\]\[a_{R,i} = a_{i+1/2}\]Now limit the data according to Eq. 1.10.
Note: you’ll need 3 ghost cells in order to compute all of the information needed.
For the method-of-lines scheme we are using, we simply evaluate the parabola on each interface and this gives that’s zones edge state. For a parabolic reconstruction in zone \(i\) of the form \(a(\xi)\), our interface states are:
\[a_{i-1/2,R} = a(\xi_{i-1/2}) = a_{L,i}\]\[a_{i+1/2,L} = a(\xi_{i+1/2}) = a_{R,i}\]Compare the solution you get with PPM for the Sod problem to the one we got with piecewise linear slopes.
