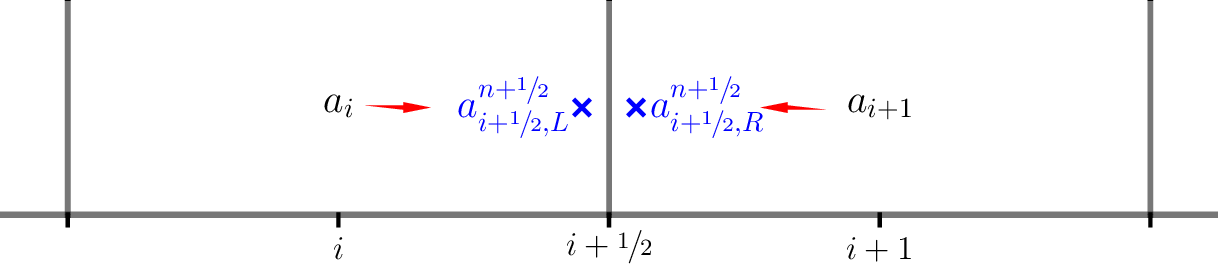Characteristic Tracing
Our finite-volume discretization left us with:
\[\frac{\partial}{\partial t} \langle a\rangle_i = -\frac{1}{\Delta x}
\left [ F_{i+1/2} - F_{i-1/2} \right ]\]
We used a method-of-lines time-update to integrate this in time. Now we’ll take a different
approach, usually referred to as characteristic tracing.
Dropping the \(\langle \cdot \rangle\), if we write the time-update using an explicit difference, we have:
\[\frac{a_i^{n+1} - a_i^n}{\Delta t} = -\frac{1}{\Delta x} \left [ F_{i+1/2} - F_{i-1/2} \right ]\]
This looks like what we had when we did our first-order accurate solver—in that case, we evaluated the fluxes at time \(n\). However, if we could find the fluxes at the midpoint in time, \(n+1/2\), then the lefthand-side would be a centered difference, and we would be second-order accurate in time:
\[\frac{a_i^{n+1} - a_i^n}{\Delta t} = -\frac{1}{\Delta x} \left [ F_{i+1/2}^{n+1/2} - F_{i-1/2}^{n+1/2} \right ]\]
and if we compute the fluxes to be second-order accurate in space, then our overall method would
be second-order accurate.
Predicting the interface states
We compute a second-order accurate flux by finding the interface state at the midpoint in time:
\[\left [f(a) \right ]_{i+1/2}^{n+1/2} = f(a_{i+1/2}^{n+1/2})\]
and we find
\(a_{i+1/2}^{n+1/2}\) by Taylor expanding the data in the cell
to the interface. The construction of the interface state at the
midpoint in time is the prediction and the conservative update in the
correction here.
\[\begin{eqnarray*}
a_{i+1/2,L}^{n+1/2} &=& a_i^n + \frac{\Delta x}{2} \left .\frac{\partial a}{\partial x} \right |_i + \frac{\Delta t}{2} \left .\frac{\partial a}{\partial t} \right |_i + \mathcal{O}(\Delta x^2) + \mathcal{O}(\Delta t^2) \\
&=& a_i^n + \frac{\Delta x}{2} \left .\frac{\partial a}{\partial x} \right |_i + \frac{\Delta t}{2} \left ( - u \left .\frac{\partial a}{\partial x} \right |_i \right ) + \ldots \\
&=& a_i^n + \frac{\Delta x}{2} \left ( 1 - \frac{\Delta t}{\Delta x} u \right ) \left .\frac{\partial a}{\partial x} \right |_i + \ldots \\
%%
a_{i+1/2,R}^{n+1/2} &=& a_{i+1}^n - \frac{\Delta x}{2} \left .\frac{\partial a}{\partial x} \right |_{i+1} + \frac{\Delta t}{2} \left .\frac{\partial a}{\partial t} \right |_{i+1} + \mathcal{O}(\Delta x^2) + \mathcal{O}(\Delta t^2) \\
&=& a_{i+1}^n - \frac{\Delta x}{2} \left .\frac{\partial a}{\partial x} \right |_{i+1} + \frac{\Delta t}{2} \left ( - u \left .\frac{\partial a}{\partial x} \right |_{i+1} \right ) + \ldots\\
&=& a_{i+1}^n - \frac{\Delta x}{2} \left ( 1 + \frac{\Delta t}{\Delta x} u \right ) \left .\frac{\partial a}{\partial x} \right |_{i+1} + \ldots
\end{eqnarray*}\]
Here we used our advection equation to replace \(\partial a/\partial t\) with \(-u \partial a/\partial x\)
We can approximate the spatial derivative in terms of the (limited) slope, \(\Delta a\):
\[\frac{\partial a}{\partial x} = \frac{\Delta a}{\Delta x}\]
and our interface states are:
\[\begin{eqnarray*}
a_{i+1/2,L}^{n+1/2} &=&
a_i^n + \frac{1}{2} \left ( 1 - \frac{\Delta t}{\Delta x} u \right ) \Delta a_i \\
%%
a_{i+1/2,R}^{n+1/2} &=&
a_{i+1}^n - \frac{1}{2} \left ( 1 + \frac{\Delta t}{\Delta x} u \right ) \Delta a_{i+1}
\end{eqnarray*}\]
Visually, for each interface, \(i+1/2\), we use data to the left (\(a_i\)) to construct
the left state and data to the right (\(a_{i+1}\)) to construct the right state:
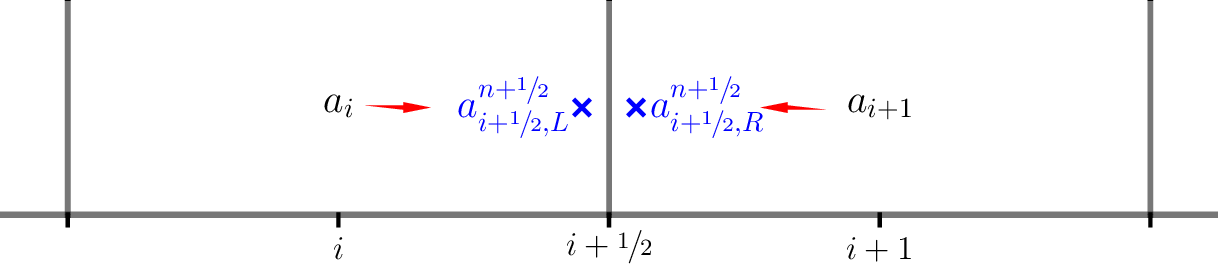
Note
Recall that the CFL number is defined as
\[C = \frac{u\Delta t}{\Delta x}\]
and is the fraction of a zone that we advect per timestep. With this
definition, we can rewrite our states as:
\[\begin{eqnarray*}
a_{i+1/2,L}^{n+1/2} &=&
a_i^n + \frac{1}{2} \left ( 1 - C \right ) \Delta a_i \\
%%
a_{i+1/2,R}^{n+1/2} &=&
a_{i+1}^n - \frac{1}{2} \left ( 1 + C \right ) \Delta a_{i+1}
\end{eqnarray*}\]
and see that the interface states are computed by just accounting for
the fraction of \(\Delta a\) that can make it to the interface over the timestep
\(\Delta t\).
Final update
We construct the left and right time-centered interface state at each interface and
then solve the Riemann problem to find the final interface state:
\[a_{i+1/2}^{n+1/2} = \mathcal{R}(a_{i+1/2,L}^{n+1/2}, a_{i+1/2,R}^{n+1/2})\]
Once this is done, we can compute the fluxes:
\[F^{n+1/2}_{i+1/2} = F(a^{n+1/2}_{i+1/2}) = u\, a^{n+1/2}_{i+1/2}\]
and then do the final conservative update as:
\[a_i^{n+1} = a_i^n + \frac{\Delta t}{\Delta x} \left ( F_{i-1/2}^{n+1/2} - F_{i+1/2}^{n+1/2} \right )\]
This result should be second-order accurate in space and time.
Try it
Code this up and compare to the method-of-lines solver.
Measure the
error and convergence rate for this solver.