Homework #9: equipotentials

Contents

Homework #9: equipotentials#

We want to plot the effective potential along the line connecting the stars.

The general potential is

(7)#\[\begin{equation} \Phi = -G \left ( \frac{M_1}{s_1} + \frac{M_2}{s_2} \right ) - \frac{1}{2} \omega^2 r^2 \end{equation}\]

This is written such that the center of mass is at the origin of coordinates. With the stars on the \(x\)-axis, the configuration looks like:

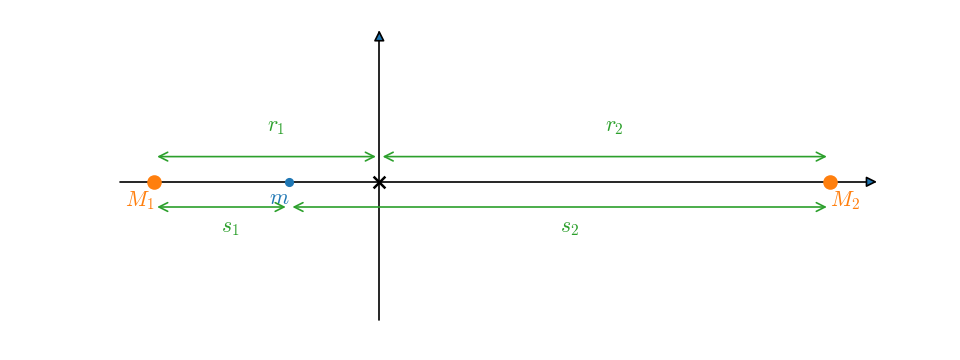
configuration of the masses

We imagine putting a test mass, \(m\), on the \(x\)-axis and asking what is the potential that it feels. Then \(s_1\) and \(s_2\) are the distances from star 1 and star 2 to the test mass, respectively, and \(r\) is the distance from the center of mass (origin) to the test mass.

a#

The center of mass condition is \(M_1 |r_1| = M_2 |r_2|\), where \(r_1\) and \(r_2\) are the distances from the star to the center of mass (the radius of their respective orbits). We also know that \(a = |r_1| + |r_2|\).

In our coordinate system, \(r_1 < 0\), so we can write this as:

(8)#\[\begin{eqnarray} -M_1 r_1 &=& M_2 r_2 \\ -r_1 + r_2 &=& a \end{eqnarray}\]

Solving this system, we get:

(9)#\[\begin{eqnarray} r_1 &=& -\frac{M_2}{M_1 + M_2} a \\ r_2 &=& \frac{M_1}{M_1 + M_2} a \end{eqnarray}\]

Now we can write down the distances, \(s_1\) and \(s_2\):

(10)#\[\begin{eqnarray} s_1 &=& | x - r_1| \\ s_2 &=& | x - r_2 | \end{eqnarray}\]

and the distance from the center of mass to our test mass, \(r\):

(11)#\[\begin{equation} r = |x| \end{equation}\]

Note that it is the distance that matters in the potential, hence we need to take absolute values.

b#

Kepler’s third law is:

(12)#\[\begin{equation} \frac{4\pi^2 a^3}{G} = (M_1 + M_2) P^2 \end{equation}\]

Recognizing that the angular velocity, \(\omega\), is \(\omega = 2\pi/P\), we have

(13)#\[\begin{equation} \omega^2 = \left (\frac{2\pi}{P} \right)^2 = \frac{G(M_1 + M_2)}{a^3} \end{equation}\]

Then we have

(14)#\[\begin{equation} \Phi = -G \left ( \frac{M_1}{|x - r_1|} + \frac{M_2}{|x - r_2|} \right ) - \frac{1}{2} \frac{G(M_1 + M_2)}{a^3} |x|^2 \end{equation}\]

c#

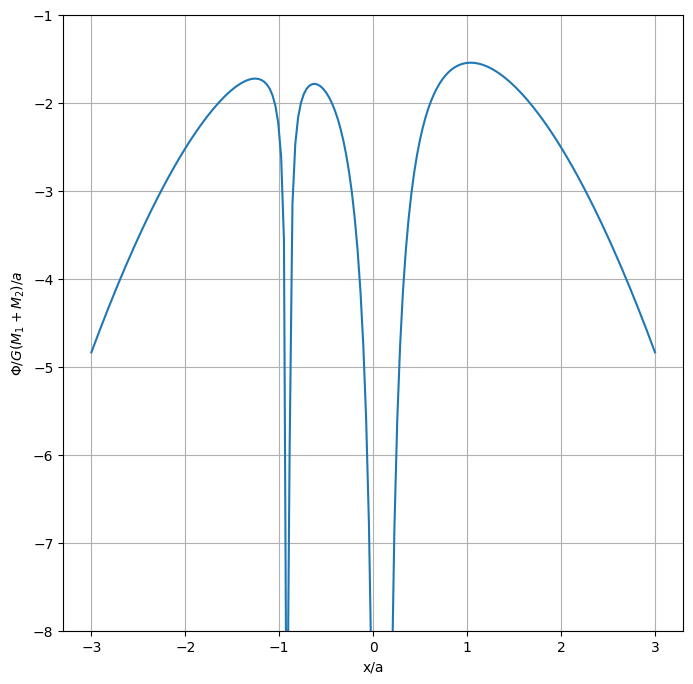
Now we want to plot our potential.

This defines the potential divided by \(G(M_1 + M_2)/a\)

import numpy as np
import matplotlib.pyplot as plt

def phi_x(x, M1, M2, a):
    r1 = -M2*a/(M1 + M2)
    r2 = M1*a/(M1 + M2)
    
    s1 = np.abs(x - r1)
    s2 = np.abs(x - r2)
    
    phi = (-(M1/s1 + M2/s2) - 0.5*(M1 + M2)/a**3 * np.abs(x)**2) / ((M1 + M2)/a)
    return phi

Define the parameters for this problem – the masses of the stars and their separation.

Msun = 2.e33
Rsun = 7.e10

M1 = 0.1*Msun
M2 = 1.0*Msun
a = Rsun

Define the range of \(x\) that we will plot

x = np.linspace(-3*a, 3*a, 200)

Now make the plot

fig = plt.figure()
fig.set_size_inches((8,8))
ax = fig.add_subplot(111)
ax.plot(x/a, phi_x(x, M1, M2, a))
ax.set_ylim(-8, -1)
ax.set_xlabel("x/a")
ax.set_ylabel(r"$\Phi / G(M_1 + M_2)/a$")
ax.grid()
../_images/20699ec89a647b7f3562fca99939a9eb35555b6e879ec65b7f79247858d4316c.png

d#

We could find the extrema approximately just by looking at the above plot, there are 3, \(x/a \sim -1\), \(x/a \sim 0.5\), \(x/a \sim 1.2\).

But I’ll find the extrema more accurately using SciPy.

First I create a wrapper to our potential function above. This will work in terms of \(x/a\), and it will also return the negative of \(\Phi\), since the SciPy routines find minima.

from scipy import optimize
def phi_min(x, M1, M2, a):
    """accept x in units of semi-major axis and return -phi, to minimize"""
    return -1 * phi_x(x*a, M1, M2, a)

Now I’ll do a bounded search – specifying the range in which I think the extrema exists. I’ll do this 3 times, once for each of the extrema.

res = optimize.minimize_scalar(phi_min, args=(M1, M2, a), method="bounded", bounds=[0.85, 2])
e1 = res.x
e1

np.float64(1.0378359067001832)

res = optimize.minimize_scalar(phi_min, args=(M1, M2, a), method="bounded", bounds=[-1, -0.1])
e2 = res.x
e2

np.float64(-0.626603891873147)

res = optimize.minimize_scalar(phi_min, args=(M1, M2, a), method="bounded", bounds=[-2, -1])
e3 = res.x
e3

np.float64(-1.2560841852731635)

Now lets plot these on our figure.

ax.scatter([e1, e2, e3],
           [phi_x(e1*a, M1, M2, a), phi_x(e2*a, M1, M2, a), phi_x(e3*a, M1, M2, a)],
           color="C1")
fig
../_images/f5cabd1123288774c7326831ecbb58b8a111ed7d3fdf47980843f2d309cde9e8.png

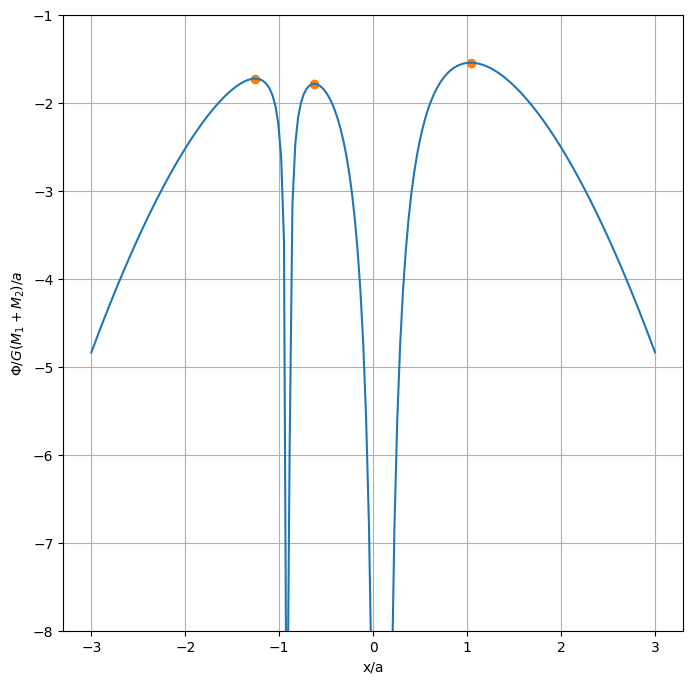
And here are the numerical values (in terms of \(x/a\))

print(e1, e2, e3)

1.0378359067001832 -0.626603891873147 -1.2560841852731635

e#

Each of the above Lagrange points are maxima, so they are unstable.

Contents