Homework #4 helium burning

This is the first problem for homework #4.

We are given the energy generation rate for helium burning via the 3-alpha reaction, and we want to understand how it behaves.

import matplotlib.pyplot as plt
import numpy as np

def q3a(T):
    """this is the triple alpha reaction rate / rho^2 Y^3"""
    T8 = T/1e8
    return 5.09e11 * T8**-3 * np.exp(-44.027/T8)

fig, ax = plt.subplots()
T = np.logspace(np.log10(3.e8), np.log10(5.e9), 100)

ax.loglog(T, q3a(T))
ax.set_xlabel("T (K)")
ax.set_ylabel(r"$q_{3\alpha}/(\rho^2 Y^3)$")
ax.grid(ls=":")

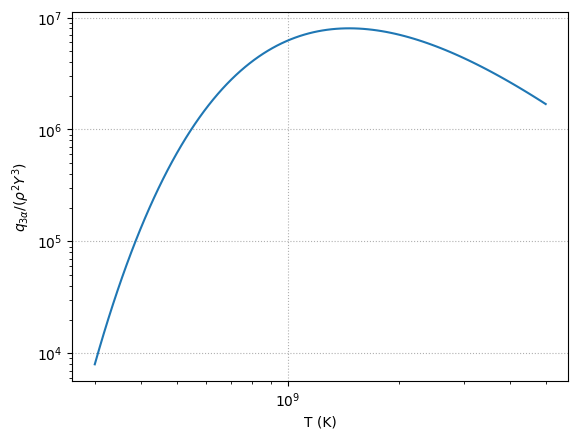
Now we want to express this as:

\[q_{3\alpha} = q_0 \rho^2 T^\nu\]

around a temperature \(T_0\).

We see that

\[\nu = \left . \frac{d\log q}{d\log T}\right |_{T_0} = \left ( \frac{T}{q} \frac{dq}{dT} \right )_{T_0}\]

Note: we don’t need to know \(\rho\) and \(Y\), because those will cancel out in the definition of \(\nu\). Also note that \(\nu\) is dimensionless.

We’ll compute this via numerical differencing. I’ll do it for a range of temperatures

print("   T        nu")
for T0 in [1.e8, 2.5e8, 5.e8, 1.e9, 2.5e9, 5e9]:
    dT = 1.e-6 * T0
    nu = (T0/q3a(T0)) * (q3a(T0 + dT) - q3a(T0))/dT
    print(f"{T0:8.5g} : {nu:5.2f}")

   T        nu
   1e+08 : 41.03
 2.5e+08 : 14.61
   5e+08 :  5.81
   1e+09 :  1.40
 2.5e+09 : -1.24
   5e+09 : -2.12

Notice that the exponent is really high for low temperatures, and it decreases for higher temperatures. At the temperature I asked for it in the homework, \(10^9~\mathrm{K}\), it is 1.4. But at a temperature of \(10^8~\mathrm{K}\), it is 41!