Exercises
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['figure.dpi'] = 100
mpl.rcParams['figure.figsize'] = (10, 8)
Exercises#
1. Euler-Cromer
A simple change to the first-order Euler method is to update the velocity first and then use the new velocity to evaluate the position:
This is called the Euler-Cromer method. In this sense, we are treating the position update implicitly.
Integrate the orbit problem with Euler-Cromer and compare to the standard Euler method. Why do you think the solutions look so different if they are both first-order?
To make things simpler, we split the RHS routine into 2, one producing the update to position and one for velocity.
G = 4*np.pi**2
M_sun = 1.0
def rhs_r(t, Y):
# unpack just to make things easier to read
x, y, vx, vy = Y
xdot = vx
ydot = vy
return np.array([xdot, ydot])
def rhs_v(t, Y):
# unpack just to make things easier to read
x, y, vx, vy = Y
r = np.sqrt(x * x + y * y)
vxdot = -G * M_sun * x / r**3
vydot = -G * M_sun * y / r**3
return np.array([vxdot, vydot])
class OrbitHistory:
"""store the time history of the orbit solution"""
def __init__(self):
self.t = []
self.x = []
self.y = []
self.vx = []
self.vy = []
def store_current_solution(self, t, Y):
self.t.append(t)
self.x.append(Y[0])
self.y.append(Y[1])
self.vx.append(Y[2])
self.vy.append(Y[3])
def plot(self, ax=None, label=None):
"""make a plot of the solution. If ax is None we setup a figure
and make the entire plot returning the figure object, otherwise, we
just append the plot to a current axis"""
fig = None
if ax is None:
fig = plt.figure()
ax = fig.add_subplot(111)
# draw the Sun
ax.scatter([0], [0], marker=(20,1), color="y", s=250)
# draw the orbit
ax.plot(self.x, self.y, label=label)
if fig is not None:
ax.set_aspect("equal")
ax.set_xlabel("x [AU]")
ax.set_ylabel("y [AU]")
return fig, ax
def initial_conditions():
x0 = 0
y0 = 1
vx0 = -np.sqrt(G*M_sun/y0)
vy0 = 0
return np.array([x0, y0, vx0, vy0])
def euler_orbit(Y0, tau, T):
# we'll return an orbit history object
o = OrbitHistory()
# storage for the new solution
Y = Y0.copy()
# initialize time
t = 0
# store the initial conditions
o.store_current_solution(t, Y0)
# main timestep loop
while t < T:
# make sure that the last step does not take us past T
if t + tau > T:
tau = T - t
# get the RHS
Rdot = rhs_r(t, Y)
Vdot = rhs_v(t, Y)
Y[0] += tau * Rdot[0]
Y[1] += tau * Rdot[1]
Y[2] += tau * Vdot[0]
Y[3] += tau * Vdot[1]
t += tau
# store the state
o.store_current_solution(t, Y)
return o
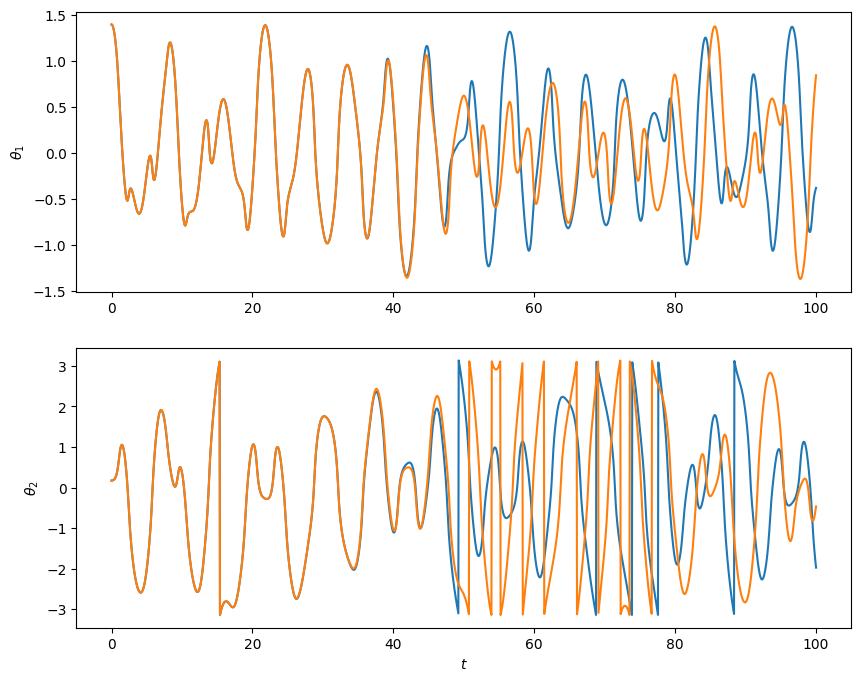
Y0 = initial_conditions()
tau = 1.0/12.0
orbit = euler_orbit(Y0, tau, 1)
orbit.plot()
(<Figure size 1000x800 with 1 Axes>, <Axes: xlabel='x [AU]', ylabel='y [AU]'>)
def euler_cromer_orbit(Y0, tau, T):
# we'll return an orbit history object
o = OrbitHistory()
# storage for the new solution
Y = Y0.copy()
# initialize time
t = 0
# store the initial conditions
o.store_current_solution(t, Y0)
# main timestep loop
while t < T:
# make sure that the last step does not take us past T
if t + tau > T:
tau = T - t
# get the RHS
Vdot = rhs_v(t, Y)
Y[2] += tau * Vdot[0]
Y[3] += tau * Vdot[1]
Rdot = rhs_r(t, Y)
Y[0] += tau * Rdot[0]
Y[1] += tau * Rdot[1]
t += tau
# store the state
o.store_current_solution(t, Y)
return o
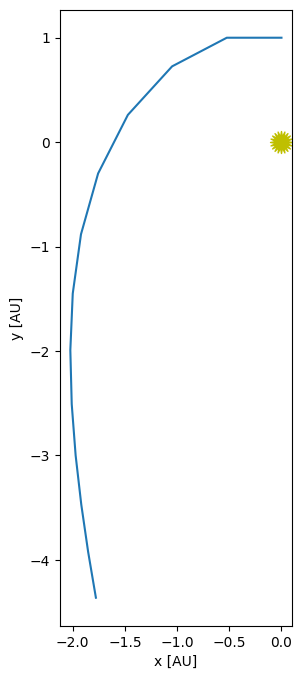
tau = 1.0/12.0
orbit = euler_cromer_orbit(Y0, tau, 1)
orbit.plot()
(<Figure size 1000x800 with 1 Axes>, <Axes: xlabel='x [AU]', ylabel='y [AU]'>)
What’s going on here? Clearly the orbit looks a lot better for Euler-Cromer than just Euler.
The reason is that Euler-Cromer actually conserves a discrete form of angular momentum, while standard Euler does not. Euler-Cromer is an example of a symplectic integrator.
2. Energy conservation
We can define the total energy / mass of our orbit system as:
since the mass of our planet does not change, this is conserved. Plot \(\mathcal{E}\) vs. time for the orbit for the different methods we looked at (including Euler-Cromer, from above). How well do they conserve energy?
3. Chaos
The equations of motion for a double pendulum consisting of two equal length rigid rods are:
where \(I = m l^2\) is the moment of inertia, \(\theta_1\) and \(\theta_2\) are the angles of the two rods with respect to the vertical and \({p_\theta}_1\) and \({p_\theta}_2\) are generalized momenta. See the wikipedia page on double pendulum for a derivation.
Write a routine to integrate this system using RK4, given initial angles \(\theta_1\) and \(\theta_2\) (take the initial momenta to be 0).
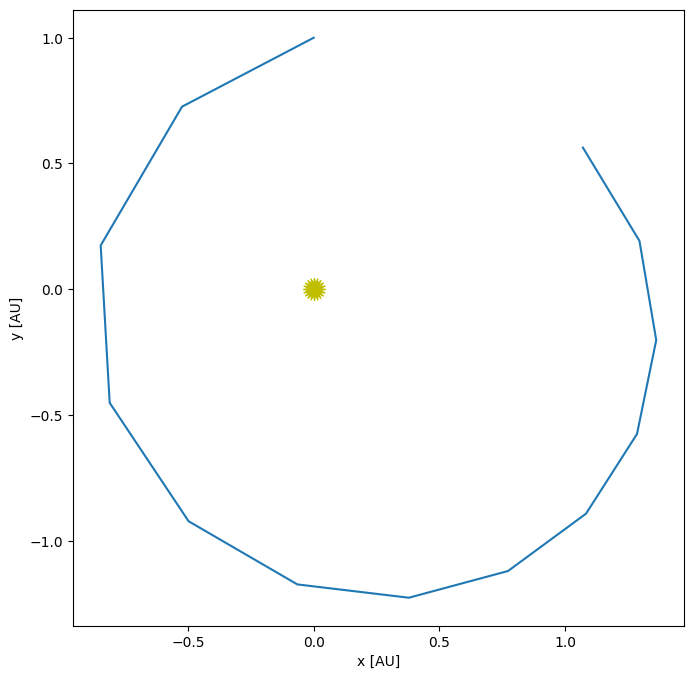
A double pendulum system is nonlinear and can exhibit chaotic behavior—the solution at some time in the future depends sensitively on the initial conditions. Make a plot of the solution you get (\(\theta_1\) and \(\theta_2\) vs. time) with two very closely spaced sets of initial conditions. What happens to the evolution?
We’ll take g = L to make it simpler. One thing we need to be careful about is that the pendulum can flip over, so we want to restrict the angles to lie between \(-\pi\) and \(\pi\)—this is accomplished by the restrict_theta() function below.
class DoublePendulum(object):
""" a class to manage and integrate the double pendulum """
def __init__(self, theta1, theta2, g=9.81, L=9.81, m=1.0):
# initial conditions
self.theta1_0 = np.radians(theta1)
self.theta2_0 = np.radians(theta2)
self.g = g
# pendula are equal length and equal mass
self.L = L
self.m = m
# final solution
self.t = None
self.theta1 = None
self.theta2 = None
def rhs(self, y):
""" equations of motion for a double compound pendulum """
theta1 = y[0]
theta2 = y[1]
p1 = y[2]
p2 = y[3]
# these are the equations of motion one gets from a Lagrangian
# approach. Note these assume a compound pendulum (e.g., a rod),
# and the moment of inertia term is that for a rod.
# moment of inertia-like term
I = self.m*self.L**2
denom = 16 - 9*np.cos(theta1 - theta2)**2
t1dot = 6/I * (2*p1 - 3*np.cos(theta1 - theta2)*p2)/denom
t2dot = 6/I * (8*p2 - 3*np.cos(theta1 - theta2)*p1)/denom
p1dot = -0.5*I*(t1dot*t2dot*np.sin(theta1 - theta2) + 3*self.g*np.sin(theta1)/self.L)
p2dot = -0.5*I*(-t1dot*t2dot*np.sin(theta1 - theta2) + self.g*np.sin(theta2)/self.L)
return np.asarray([t1dot, t2dot, p1dot, p2dot])
def integrate(self, dt, tmax):
""" integrate the equations of motion using the RK4 """
# initial conditions
t = 0.0
theta1 = self.theta1_0
theta2 = self.theta2_0
# start out at rest
p1 = 0.0
p2 = 0.0
# store the history for plotting
t_points = [t]
theta1_points = [theta1]
theta2_points = [theta2]
y = np.asarray([theta1, theta2, p1, p2])
while t < tmax:
# get the RHS at time-level n
k1 = self.rhs(y)
k2 = self.rhs(y + 0.5*dt*k1)
k3 = self.rhs(y + 0.5*dt*k2)
k4 = self.rhs(y + dt*k3)
ynew = y + dt/6.0 * (k1 + 2*k2 + 2*k3 + k4)
t += dt
# restrict theta
ynew[0] = self.restrict_theta(ynew[0])
ynew[1] = self.restrict_theta(ynew[1])
# store
t_points.append(t)
theta1_points.append(ynew[0])
theta2_points.append(ynew[1])
# set for the next step
y[:] = ynew[:]
# store the entire solution
self.t = np.asarray(t_points)
self.theta1 = np.asarray(theta1_points)
self.theta2 = np.asarray(theta2_points)
def restrict_theta(self, theta):
"""convert theta in place to be restricted to lie between -pi and pi.
This is done in a periodic fashion, with theta' = theta +/- 2n
pi
"""
# shift everything by pi, then restrict to lie between [0,
# 2pi], then shift back by pi
theta += np.pi
theta += - 2.0*np.pi*np.floor(theta/(2.0*np.pi))
theta -= np.pi
return theta
dt = 0.05
tmax = 100.0
# run two double pendula with very close initial conditions
# they will diverge after some time
p_a = DoublePendulum(80, 10)
p_a.integrate(dt, tmax)
p_b = DoublePendulum(80.0001, 10.0001)
p_b.integrate(dt, tmax)
fig = plt.figure()
ax = fig.add_subplot(211)
ax.plot(p_a.t, p_a.theta1)
ax.plot(p_b.t, p_b.theta1)
ax.set_ylabel(r"$\theta_1$")
ax = fig.add_subplot(212)
ax.plot(p_a.t, p_a.theta2)
ax.plot(p_b.t, p_b.theta2)
ax.set_xlabel(r"$t$")
ax.set_ylabel(r"$\theta_2$")
Text(0, 0.5, '$\\theta_2$')