from sympy import init_session
init_session()

IPython console for SymPy 1.11.1 (Python 3.10.9-64-bit) (ground types: python)

These commands were executed:
>>> from sympy import *
>>> x, y, z, t = symbols('x y z t')
>>> k, m, n = symbols('k m n', integer=True)
>>> f, g, h = symbols('f g h', cls=Function)
>>> init_printing()

Documentation can be found at https://docs.sympy.org/1.11.1/

Euler equations eigensystem

Primitive variable form

The Euler equations in primitive variable form, \({\bf q} = (\rho, u, p)^\intercal\) appear as:

\[{\bf q}_t + {\bf A}({\bf q}) {\bf q}_x = 0\]

with the matrix \({\bf A}({\bf q})\):

\[\begin{split}{\bf A}({\bf q}) = \left ( \begin{array}{ccc} u & \rho & 0 \\ 0 & u & 1/\rho \\ 0 & \gamma p & u \end{array} \right ) \end{split}\]

The sound speed is related to the adiabatic index, \(\gamma\), as \(c^2 = \gamma p /\rho\).

We can represent this matrix symbolically in SymPy and explore its eigensystem.

from sympy.abc import rho
rho, u, c = symbols('rho u c')

A = Matrix([[u, rho, 0], [0, u, rho**-1], [0, c**2 * rho, u]])
A

\[\begin{split}\displaystyle \left[\begin{matrix}u & \rho & 0\\0 & u & \frac{1}{\rho}\\0 & c^{2} \rho & u\end{matrix}\right]\end{split}\]

The eigenvalues are the speeds at which information propagates with. SymPy returns them as a dictionary, giving the multiplicity for each eigenvalue.

A.eigenvals()

The right eigenvectors are what SymPy gives natively. For a given eigenvalue, \(\lambda\), these satisfy:

\[{\bf A} {\bf r} = \lambda {\bf r}\]

Right Eigenvectors

R = A.eigenvects()   # this returns a tuple for each eigenvector with multiplicity -- unpack it
r = []
lam = []
for (ev, _, rtmp) in R:
    r.append(rtmp[0])
    lam.append(ev)
    
# we can normalize them anyway we want, so let's make the first entry 1
for n in range(len(r)):
    v = r[n]
    r[n] = v/v[0]

0-th right eigenvector

r[0]

\[\begin{split}\displaystyle \left[\begin{matrix}1\\0\\0\end{matrix}\right]\end{split}\]

this corresponds to the eigenvalue

lam[0]

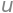
1-st right eigenvector

r[1]

\[\begin{split}\displaystyle \left[\begin{matrix}1\\- \frac{c}{\rho}\\c^{2}\end{matrix}\right]\end{split}\]

this corresponds to the eigenvalue

lam[1]

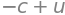
2-nd right eigenvector

r[2]

\[\begin{split}\displaystyle \left[\begin{matrix}1\\\frac{c}{\rho}\\c^{2}\end{matrix}\right]\end{split}\]

this corresponds to the eigenvalue

lam[2]

Here they are as a matrix, \({\bf R}\), in order from smallest to largest eigenvalue

R = zeros(3,3)
R[:,0] = r[1]
R[:,1] = r[0]
R[:,2] = r[2]
R

\[\begin{split}\displaystyle \left[\begin{matrix}1 & 1 & 1\\- \frac{c}{\rho} & 0 & \frac{c}{\rho}\\c^{2} & 0 & c^{2}\end{matrix}\right]\end{split}\]

Left Eigenvectors

The left eigenvectors satisfy:

\[{\bf l} {\bf A} = \lambda {\bf l}\]

We’ll find these by taking the transpose of \({\bf A}\)

\[({\bf l} {\bf A})^\intercal = {\bf A}^\intercal {\bf l}^\intercal = \lambda {\bf l}^\intercal\]

Therefore, the transpose of the left eigenvectors, \({\bf l}^\intercal\), are the right eigenvectors of transpose of \({\bf A}\)

B = A.transpose()
B

\[\begin{split}\displaystyle \left[\begin{matrix}u & 0 & 0\\\rho & u & c^{2} \rho\\0 & \frac{1}{\rho} & u\end{matrix}\right]\end{split}\]

L = B.eigenvects()
l = []
laml = []
for (ev, _, ltmp) in L:
    l.append(ltmp[0].transpose())
    laml.append(ev)
    

Traditionally, we normalize these such that \(l^{(\mu)} \cdot r^{(\nu)} = \delta_{\mu\nu}\)

for n in range(len(l)):
    if lam[n] == laml[n]:
        ltmp = l[n]
        p = ltmp.dot(r[n])
        l[n] = ltmp/p

0-th left eigenvector

l[0]

\[\displaystyle \left[\begin{matrix}1 & 0 & - \frac{1}{c^{2}}\end{matrix}\right]\]

1-st left eigenvector

l[1]

\[\displaystyle \left[\begin{matrix}0 & - \frac{\rho}{2 c} & \frac{1}{2 c^{2}}\end{matrix}\right]\]

2-nd left eigenvector

l[2]

\[\displaystyle \left[\begin{matrix}0 & \frac{\rho}{2 c} & \frac{1}{2 c^{2}}\end{matrix}\right]\]

Entropy formulation

here we write the system in terms of \({\bf q}_s = (\rho, u, s)^\intercal\), where the system is

\[{{\bf q}_s}_t + {\bf A}_s({\bf q}_s) {{\bf q}_s}_x = 0\]

and

\[\begin{split} {\bf A}_s = \left (\begin{matrix}u & \rho & 0\\ \frac{c^{2}}{\rho} & u & \frac{p_{s}}{\rho}\\ 0 & 0 & u\end{matrix}\right) \end{split}\]

ps = symbols('p_s')

As = Matrix([[u, rho, 0], [c**2/rho, u, ps/rho], [0, 0, u]])
As

\[\begin{split}\displaystyle \left[\begin{matrix}u & \rho & 0\\\frac{c^{2}}{\rho} & u & \frac{p_{s}}{\rho}\\0 & 0 & u\end{matrix}\right]\end{split}\]

As.eigenvals()

R = As.eigenvects()   # this returns a tuple for each eigenvector with multiplicity -- unpack it
r = []
lam = []
for (ev, _, rtmp) in R:
    r.append(rtmp[0])
    lam.append(ev)
    
# we can normalize them anyway we want, so let's make the first entry 1
for n in range(len(r)):
    v = r[n]
    r[n] = v/v[0]

r[0]

\[\begin{split}\displaystyle \left[\begin{matrix}1\\0\\- \frac{c^{2}}{p_{s}}\end{matrix}\right]\end{split}\]

this corresponds to eigenvalue

lam[0]

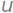
r[1]

\[\begin{split}\displaystyle \left[\begin{matrix}1\\- \frac{c}{\rho}\\0\end{matrix}\right]\end{split}\]

this corresponds to eigenvalue

lam[1]

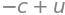
r[2]

\[\begin{split}\displaystyle \left[\begin{matrix}1\\\frac{c}{\rho}\\0\end{matrix}\right]\end{split}\]

this corresponds to eigenvalue

lam[2]

left eigenvectors

Bs = As.transpose()
L = B.eigenvects()
l = []
laml = []
for (ev, _, ltmp) in L:
    l.append(ltmp[0].transpose())
    laml.append(ev)
    

normalization

for n in range(len(l)):
    if lam[n] == laml[n]:
        ltmp = l[n]
        p = ltmp.dot(r[n])
        l[n] = ltmp/p

simplify(l[0])

\[\displaystyle \left[\begin{matrix}\frac{p_{s}}{p_{s} + 1} & 0 & - \frac{p_{s}}{c^{2} \left(p_{s} + 1\right)}\end{matrix}\right]\]

l[1]

\[\displaystyle \left[\begin{matrix}0 & - \frac{\rho}{c} & \frac{1}{c^{2}}\end{matrix}\right]\]

l[2]

\[\displaystyle \left[\begin{matrix}0 & \frac{\rho}{c} & \frac{1}{c^{2}}\end{matrix}\right]\]