Homework 3 solutions#
We want to integrate the simple pendulum without the small angle approximation and compare different integration schemes
import numpy as np
import matplotlib.pyplot as plt
class SimplePendulum:
""" manage and integrate a simple pendulum """
def __init__(self, theta0, g=9.81, L=9.81, method="Euler"):
"""we'll take theta0 in degrees and assume that the angular
velocity is initially 0"""
# initial condition
self.theta0 = np.radians(theta0)
self.g = g
self.L = L
def energy(self, theta_vec, omega_vec):
""" given a solution, return the energy (per unit mass) """
return 0.5 * self.L**2 * omega_vec**2 - self.g * self.L * np.cos(theta_vec)
def period(self):
""" return an estimate of the period, up to the theta**2 term """
return 2.0 * np.pi * np.sqrt(self.L / self.g) * (1.0 + self.theta0**2 / 16.0)
def rhs(self, theta, omega):
""" equations of motion for a pendulum
dtheta/dt = omega
domega/dt = - (g/L) sin theta """
return np.array([omega, -(self.g / self.L) * np.sin(theta)])
def integrate_euler(self, dt, tmax):
""" integrate the equations of motion using Euler's method """
# initial conditions
t = 0.0
t_s = [t]
theta_s = [self.theta0]
omega_s = [0.0]
while t < tmax:
# initial state
theta = theta_s[-1]
omega = omega_s[-1]
# get the RHS
thetadot, omegadot = self.rhs(theta, omega)
# advance
theta_new = theta + dt * thetadot
omega_new = omega + dt * omegadot
t += dt
# store
t_s.append(t)
theta_s.append(theta_new)
omega_s.append(omega_new)
return np.array(t_s), np.array(theta_s), np.array(omega_s)
def integrate_ec(self, dt, tmax):
""" integrate the equations of motion using the Euler-Cromer method """
# initial conditions
t = 0.0
t_s = [t]
theta_s = [self.theta0]
omega_s = [0.0]
while t < tmax:
# initial state
theta = theta_s[-1]
omega = omega_s[-1]
# get the RHS
thetadot, omegadot = self.rhs(theta, omega)
# advance
omega_new = omega + dt * omegadot
theta_new = theta + dt * omega_new
t += dt
# store
t_s.append(t)
theta_s.append(theta_new)
omega_s.append(omega_new)
return np.array(t_s), np.array(theta_s), np.array(omega_s)
def integrate_vv(self, dt, tmax):
""" integrate the equations of motion using velocity Verlet method """
# initial conditions
t = 0.0
t_s = [t]
theta_s = [self.theta0]
omega_s = [0.0]
while t < tmax:
# initial state
theta = theta_s[-1]
omega = omega_s[-1]
# get the RHS at time-level n
thetadot, omegadot = self.rhs(theta, omega)
omega_half = omega + 0.5 * dt * omegadot
theta_new = theta + dt * omega_half
# get the RHS with the updated theta -- omega doesn't matter
# here, since we only need thetadot and omega doesn't affect
# that.
_, omegadot_new = self.rhs(theta_new, omega)
omega_new = omega_half + 0.5 * dt * omegadot_new
t += dt
# store
t_s.append(t)
theta_s.append(theta_new)
omega_s.append(omega_new)
return np.array(t_s), np.array(theta_s), np.array(omega_s)
Let’s try it out
Case 1: \(\theta_0 = 10^\circ\)#
# initial angle in degrees -- the class converts to radians
theta0 = 10
p10 = SimplePendulum(theta0)
period = p10.period()
print(f"{period=}")
period=6.295147605281553
Euler’s method
# fixed timestep
dt = 0.1
tmax = 10 * period
t_euler, theta_euler, omega_euler = p10.integrate_euler(dt, tmax)
fig, ax = plt.subplots()
ax.plot(t_euler, theta_euler, label="Euler")
ax.set_xlabel("t [s]")
ax.set_ylabel(r"$\theta$")
ax.grid()
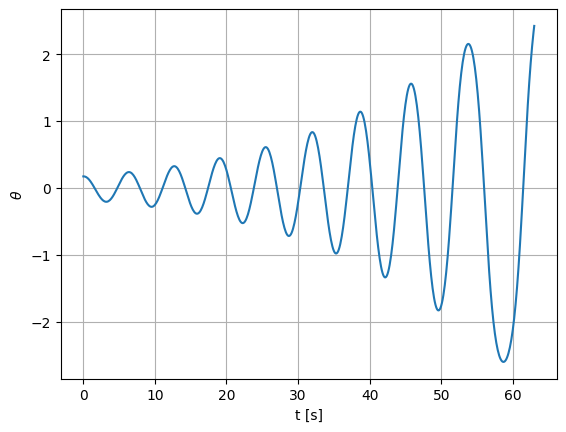
Now let’s do Euler-Cromer
t_ec, theta_ec, omega_ec = p10.integrate_ec(dt, tmax)
ax.plot(t_ec, theta_ec, label="Euler-Cromer")
ax.legend()
fig
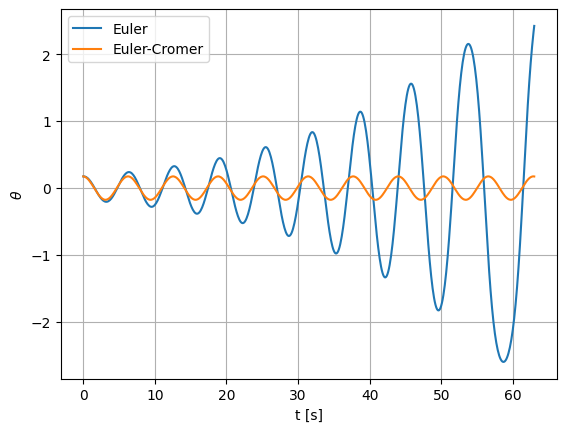
finally velocity-Verlet
t_vv, theta_vv, omega_vv = p10.integrate_vv(dt, tmax)
ax.plot(t_vv, theta_vv, label="velocity-Verlet")
ax.legend()
fig
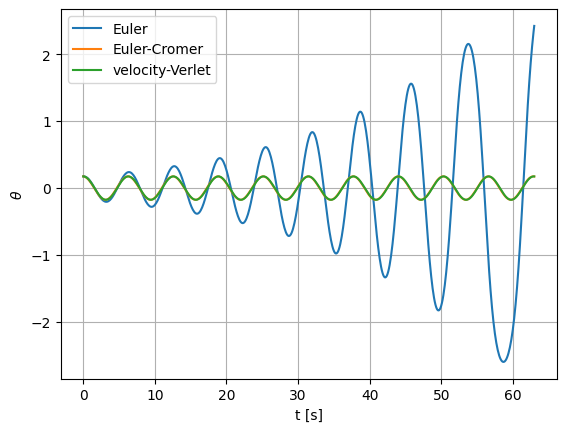
We see that the Euler-Cromer and velocity-Verlet solutions look the same, and the amplitude of the pendulum does not change noticeably with time—as expected, since there is no damping in the system.
Let’s look at energy
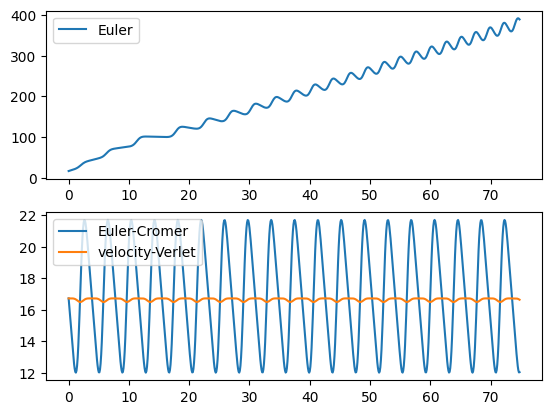
E_euler = p10.energy(theta_euler, omega_euler)
E_ec = p10.energy(theta_ec, omega_ec)
E_vv = p10.energy(theta_vv, omega_vv)
fig = plt.figure()
ax1 = fig.add_subplot(211)
ax1.plot(t_euler, E_euler, label="Euler")
ax1.legend()
ax2 = fig.add_subplot(212)
ax2.plot(t_ec, E_ec, label="Euler-Cromer")
ax2.plot(t_vv, E_vv, label="velocity-Verlet")
ax2.legend()
<matplotlib.legend.Legend at 0x7f99a8631ed0>
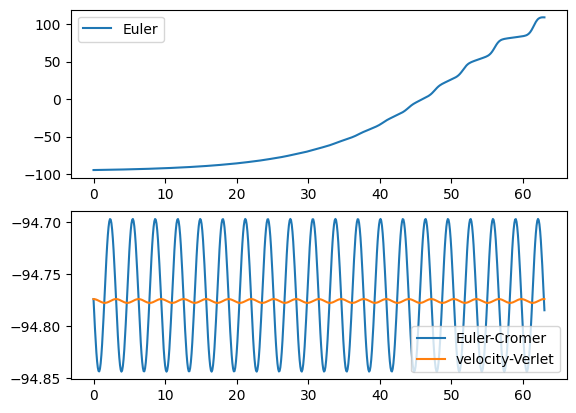
Here we see that the energy conservation in Euler is really bad.
Case 2: \(\theta_0 = 100^\circ\)#
theta0 = 100
p100 = SimplePendulum(theta0)
period = p100.period()
print(f"{period=}")
period=7.479415117376338
Notice that the period here is very different than the classic small-angle approximation period.
# fixed timestep
dt = 0.1
tmax = 10 * period
t_euler, theta_euler, omega_euler = p100.integrate_euler(dt, tmax)
t_ec, theta_ec, omega_ec = p100.integrate_ec(dt, tmax)
t_vv, theta_vv, omega_vv = p100.integrate_vv(dt, tmax)
fig, ax = plt.subplots()
ax.plot(t_euler, theta_euler, label="Euler")
ax.plot(t_ec, theta_ec, label="Euler-Cromer")
ax.plot(t_vv, theta_vv, label="velocity-Verlet")
ax.legend()
ax.set_xlabel("t [s]")
ax.set_ylabel(r"$\theta$")
ax.set_ylim(-8, 3)
ax.grid()
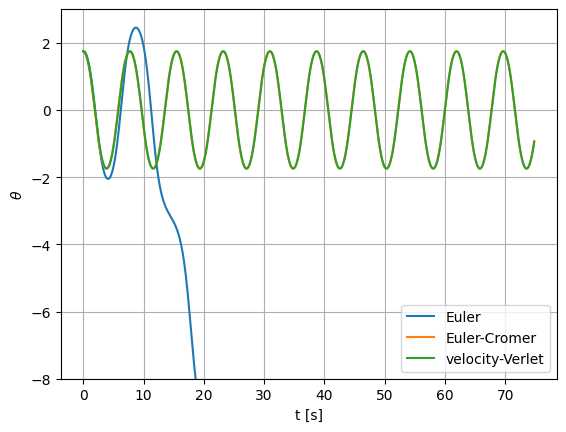
Again, the Euler-Cromer and velocity-Verlet methods track nicely
E_euler = p100.energy(theta_euler, omega_euler)
E_ec = p100.energy(theta_ec, omega_ec)
E_vv = p100.energy(theta_vv, omega_vv)
fig = plt.figure()
ax1 = fig.add_subplot(211)
ax1.plot(t_euler, E_euler, label="Euler")
ax1.legend()
ax2 = fig.add_subplot(212)
ax2.plot(t_ec, E_ec, label="Euler-Cromer")
ax2.plot(t_vv, E_vv, label="velocity-Verlet")
ax2.legend()
<matplotlib.legend.Legend at 0x7f99a85b3160>